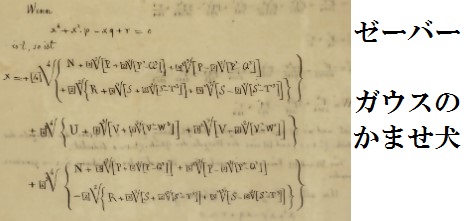数学者としてのゼーバー-ガウスのかませ犬

今回は「ガウスのかませ犬」といわれてしまったゼーバーの人生について、詳しく説明する。また、彼の業績についても取り上げる。

ゼーバー：
2次形式に関する値の上限が3以下であることを、600個の例を使って示しました。本当は上限は2以下だと思いますが。

（匿名で）
帰納的に頑張ったみたいだけど、1ページ半の証明で上限が2より小さいことが示せたよ。すでに「算術考究」の中でやったけどね。

みんな：
あいつだ・・・

歴史と考察
1. 発明発見の背景
ゼーバーの生涯
1. 発明発見の意義
感想
豆知識
おすすめ

歴史と考察

ガウスの同時代にルートヴィヒ・ゼーバーという研究者がいた。この人物はケプラー予想に関係のある問題を証明しようとしたが、弱い条件の問題しか証明できなかった。これを読んだガウスは、書評にて完璧な証明をしめし、この書評は有名になった。これをきっかけに、ゼーバーは「かませ犬」といわれるようになってしまった。
　ゼーバーの生涯を年表にした。また、彼の功績を記すことで名誉の回復としたい。なお、彼は物理学者・結晶学者であり、数学者が本業というわけではなかったということは書いておくべきだろう。

発明発見の背景

まだこの時代にはケプラー予想は解決されていない。この予想はまず球が規則正しい並び方をした場合のケースから証明されるがそれもまだである。

ゼーバーの生涯

1793年に、ルートヴィヒ・アウグスト・ゼーバーはドイツで生まれた。実は、学業の過程でガウスの指導を受けたこともあったらしい。1819ねんには、カールスルーエで教師になる。
問題の論文は1831年に出た。ゼーバーはこの年に「正値3変数2次形式の諸性質について」を出版。このなかでは600程度の可能性を計算し、予想を立てた。それをもとに証明を試みたが、弱い条件の証明しかできなかった。これに割いたページ数はなんと248ページにおよんだ。証明には91ページ使っている。

　ゼーバーのアプローチは上述の通り、数百の可能性について論考を重ね、最終的に成り立つであろう証明を組み立てている。これは、どちらかというと帰納法のようなな方法で、数学者の直感的なやり方というよりは、いかにも物理学者らしいと言えるかもしれない。
　もし、ゼーバーがガウスのアリトメティカ考究を読んでいたら、もしかしたら一発でガウスのような証明ができていたかも？！

　1831年7月には、ガウスはこの証明を読み、書評を書いた。たった1ページ半の証明で、計算は40行ほどだった。これにより当初証明されるべきだった予想（条件を弱めない問題）を証明した。
　なお、この時ガウスは匿名で書いたのだが、「算術考究」にふれているのと、その一切無駄のない文体から、ガウスであるとすぐばれた。
　最後にはおきまりの「すでに自分が昔やった」とアピール。（これもガウスがよくやっていたアピールである）

ゼーバーはそれなりにショックを受けたようだが、その後も研究者のキャリアを続けた。
1834年には、ゼーバーはフライブルク大学で物理学の教授になり1840年まで同職についた。その後、1855年にゼーバー、死去。

ゼーバーの功績
・かれの功績は結晶学に関する個体の構造についての研究で、今日の結晶学でも参考にされている。・また、ケプラー予想の問題を通じて、2次形式を簡約にするアルゴリズムをつくった。

発明発見の意義

ゼーバーにはかわいそうなことになってしまったが、かれはガウスの計算を引き出したという意味でケプラー予想の解決に貢献したということができる。

感想

・なぜゼーバーはケプラー予想に挑んだのか？
　彼はケプラー予想のうち、予想の基礎となるような部分的な問題に挑んだに過ぎないので、ケプラー予想に挑んだと書くと少し大げさかもしれない。これは、おそらく結晶の並び方について考えているときに、ケプラー予想と似たような、球体の並び方に対する問題に突き当たったためであると考えられる。

・ゼーバーはガウスの書評をどううけとったのか？
ガウスは、すでに自分がやったというかたちで、書評を書いているものの、文体自体は冷静で、ゼーバーを見下したような様子は見られないということらしい。これはゼーバーにとって、いくらか救われたのではないだろうか。ゼーバーも当時最高峰の頭脳と認められていたガウスから書評を受けるのは、批判的な内容であったとしても嬉しい反論であったかもしれない。
　ただ、後年までガウスの咬ませ犬という評価を付けられてしまったのは少しかわいそうな気もする。

豆知識

・ゼーバーは1855年に亡くなったが、これはガウスがなくなったのと同じ年である。奇妙な一致である。

・ガウスはケプラー予想に貢献したものの、この時代にまだ未解決だったフェルマーの最終定理には手を付けていない。

歴史と考察

発明発見の背景

ゼーバーの生涯

発明発見の意義

感想

豆知識

おすすめ