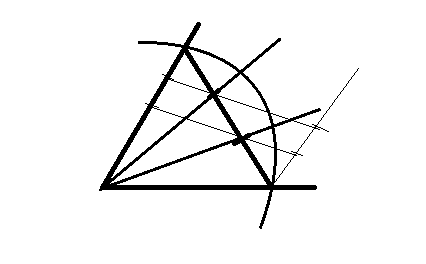
不可能な作図問題の代表例として知られる角の3等分。ただし歴史上には、解いたという主張をする人があとを立たなかった。この失敗の歴史について解説する。関連:ネウシス作図!定規・コンパスのみで角の三等分【動画】-作図可能な具体例
歴史と考察
定規とコンパスを使った作図のうち、長い間難問とされていたのが「角の3等分」である。その歴史は古代ギリシアから始まっている。19世紀にようやく不可能性が証明された。しかしながら、三等分できると主張する人がその後もニュースになるなど、お騒がせな問題であった。現代でも、頑張って三等分しようとするひとがいるようである。
発見の背景
紀元前5~6世紀、作図の三大難問がとかれはじめる。この時は、円の正方形化と立方倍積問題も不可能性は証明されておらず、一緒に取り組まれていた。 角の3等分ではなく直線の3等分であればたやすくできるので、一見、角もたやすくできそうに思える。
不可能への挑戦
15世紀にデューラーが、3等分ではないが近似する方法を発見する。これをデューラー法という。これはわりと簡便な作図法でありながら、精度は結構よい。デューラーは数学的素養があり、真の3等分ではないことがわかっていたと思われる。
19世紀までにコップ=ペロン法が開発される。これはデューラー法の精度改良を目指したもので、さらに近い値が得られる。
1837についにワンツェル(ヴァンツェル)によって、3等分が不可能であると証明された。定規とコンパスによる作図は、2のべき乗の方程式を解くことと同じであり、角の三等分という3次方程式をコンパスと定規で解くことはできないと判明した。
数学的に不可能とわかったのに・・・
19世紀半ば、フランスアカデミーが、「角の3等分と永久機関の論文は受け付けない」と発表する。逆に言うと、そのような論文が出され続けていたということである。
さらに19世紀には、ド・モルガンが「パラドックサーの群」を出版、「3等分を試みる人がいることは極めて悲しむべきもの」と述べる。
1931に、最大のお騒がせ事件が起こる。カラハン神父が、角の3等分と解決と主張した。タイム誌や新聞にものったが、元の角度を3倍して、その角度の3等分ができた(つまり元の角度を作図した)というものに過ぎなかった。

こののちも騒動はあり、1959年には画家のキジュールとヤングが、解決を主張した。これは近似的な作図とおもわれる。1966年ロサンゼルスの新聞に3等分に成功したとのる。こちらも勘違いか、近似であろう。
1983に極め付けだが、「3等分屋が来たらどう対応すればよいか」を指南する論文がでている。
なお、日本では、明治18年「東洋学芸雑誌」に厳密な不可能証明の募集がされており、まだ証明が広くは知られていなかったことがうかがえる。明治22には、「未だに月に2,3個は3等分できたとの証明が送られてくる。暇な人もいるものだ」という言説が載っている。
発明発見の意義
この発見への挑戦は不可能ということで決着がついたが、3等分のための器具がシュシュ考案された。このことは成果といってよいだろう。
豆知識
なお、現代でも3等分を夢見る人がおり、「3等分屋(トライセクター)」と言われている。
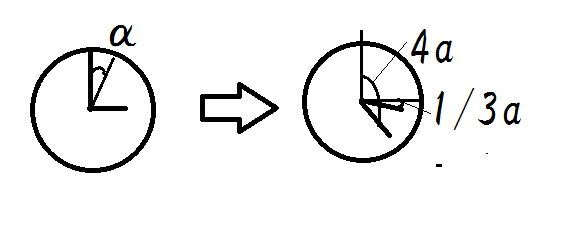
・アナログ時計を使うと3等分ができる。時計の分針が三等分したい角の4倍になったとき、時針が元の角の3等分になっている。
おすすめ
- 丙午(ひのえうま)の迷信と女性の出産‐次は2026年!
- 錬金術が死んだ日-ある錬金術師の自殺と原子論
- ネウシス作図!定規・コンパスのみで角の三等分【動画】-作図可能な具体例
- 偽メシアの外れた予言まとめ
- 財政破綻論の外れ続けた予言まとめ
- 反重力・重力を遮断する物質が発見された?!
- 角の3等分の方法が発見された?!
- カントールと無限と教会
- フロギストン説とカロリック説の欠点・問題点-燃素・熱素
- バチビウス-あらゆる生物の祖先?
考察
・なぜ3等分屋はいなくならないのか?
角の3等分を試みる人たちが消えていなくならないのは、以下の理由によると考えられる。
・不可能性の証明が理解できない
・近似を勘違いした
・何かしらの名声がほしい
・三等分できる角
実は90°、つまり直角は三等分することができる。これは、正三角形が作図できるからで、それを作図した後に正三角形の内閣を2等分すれば、角の内訳が30度ずつになるので三相分となる。
よって、45度も三等分できる。これは一度90度に角度を直して三等分し、さらに2等分すればよいからである。また、22.5°も三等分できる。
このように考えると、あらかじめ角度がわかっていれば、三等分できる角は無限に存在することがわかる。これは、他の作図の問題にはない特徴であると言えるだろう。