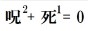方程式の解の公式はどのように発見されていったのかの年表。1次方程式、2次方程式の解の公式は古代から知られていたが、3次方程式までに実に3000年近い時間の開きがある。なお、本文中に示した解の公式は、未知数にに記号がついていない場合のものである。
3次以降の解の公式にかかわった人は、みな不幸な死に方をしているのが何とも不気味である。
年表
1次方程式の解の公式
1次方程式にも一応、解の公式ともいえるものはある。
紀元前1700年ごろ:アーメス・パピルス、1次方程式の解の公式が残されている。おそらく数学に関心のある書記官が記したものと思われる。

2次方程式の解の公式
紀元前1600年代:バビロニアの文書に2次方程式の解の公式が示されている。こちらもおそらく数学に関心のある書記官が記したものと思われる。
古代インド:負の数を入れることで2次方程式を簡略化。負の数の概念によって、わざわざ場合分けして書かなくても記述できることが示された。
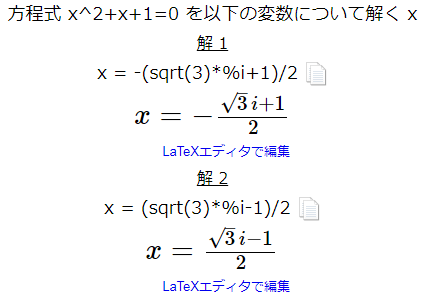
3次方程式の解の公式
3次方程式は、明確に誰が発見者か判明している。もっとも、いざこざがあった。
1540代:フォンタナ、3次方程式の解の公式を見つける。これを秘密にするという約束でカルダーノに教えた。
1545:カルダーノ、「アルス・マグナ」で発表。 このため、カルダーノの公式として知られる。
直後:フォンタナは激怒。なお、カルダーノは自分の占星術の予言どおりに死ぬため、予言された日に自殺したと言われている。
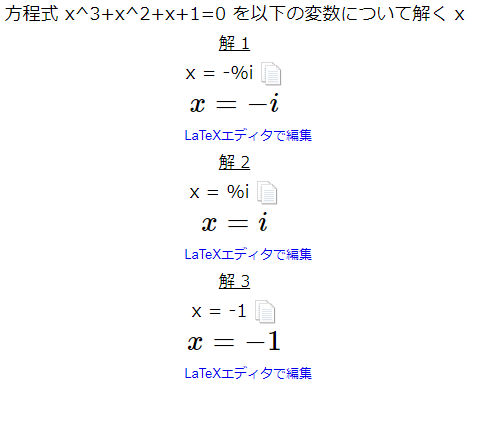
4次方程式の解の公式
4次方程式も、明確に誰が発見者か判明している。
16世紀:カルダーノの弟子フェラーリ、4次方程式の解の公式を見つける。

5次方程式の解の公式が存在しないことの証明
5次方程式については、解の公式が一般には存在しないことで決着がついた。
1820:アーベル、一般的な5次方程式の解の公式はないことを証明。
1829:アーベル、病で若くして死去。
1830年代:ガロア、解の公式が作れる場合とそうでない場合の条件を確定する。5次方程式に関する厳密な考え方を整備した。
1832:ガロア、決闘で若くして死去。
豆知識
・現代数学に大きな貢献をしたアーベルだったが、教員に任命される手紙の届く二日前に亡くなった。
・ガロアの最後の言葉は、駆け付けた弟がなくのを見て「なくな、20歳で死ぬということはありったけの勇気が必要なのだから」であったらしい。
おすすめ
- 素数の公式『ミルズの公式&ミルズ定数』定数をかけるだけで素数が?
- 四色問題の証明は美しくない?!批判と反論まとめ!実は美しい証明もあった!
- 正17角形の簡単な作図方法!10分でできる!定規とコンパスで描いてみよう
- 素数の公式『ウィランズの公式』解説!ウィルソンの定理との関係も!
- スメイルの問題全部解説するまで帰れま18記事一覧
- 微分同相写像とリー群モデルの関係とは?スメイルの問題全部解説するまで帰れま18(番外編3)
- 三次元球面は最小集合?スメイルの問題全部解説するまで帰れま18(番外編2)
- 平均値問題とは?スメイルの問題全部解説するまで帰れま18(番外編1)
- 人間と人工知能の知能の限界とは?スメイルの問題全部解説するまで帰れま18(18)
- 多項式を平均多項式時間で解くとは?スメイルの問題全部解説するまで帰れま18(17)
- ヤコビアン予想とは?スメイルの問題全部解説するまで帰れま18(16)
- ローレンツアトラクターの特性とは?スメイルの問題全部解説するまで帰れま18(14)
- 微分同相写像の中心化群とは?スメイルの問題全部解説するまで帰れま18(12)
- 1次元力学系は一般に双曲型?スメイルの問題全部解説するまで帰れま18(11)
- Pughの閉補題とは?日本の研究者も活躍!スメイルの問題全部解説するまで帰れま18(10)
- 線形計画問題とは?スメイルの問題全部解説するまで帰れま18(9)
- 経済学理論への力学の導入とは?スメイルの問題全部解説するまで帰れま18(8)
- 2-球面上の点の分布とは?スメイルの問題全部解説するまで帰れま18(7)
- 天体力学における相対平衡数の有限性とは?スメイルの問題全部解説するまで帰れま18(6)
- ディオファントス曲線の高さ境界とは?スメイルの問題全部解説するまで帰れま18(5)
- 1変数多項式の整数零点についてのτ予想とは?スメイルの問題全部解説するまで帰れま18(4)
- ヒルベルトの23の問題全部解説するまで帰れま23記事一覧
- ヒルベルトの24番目の問題とは?隠された謎とその内容に迫る!
- 変分法の研究の展開とは?ヒルベルトの23の問題全部解説するまで帰れま23(23)
- 保型関数による解析関数の一意化とは?ヒルベルトの23の問題全部解説するまで帰れま23(22)
- モノドロミー群をもつ線型微分方程式とは?ヒルベルトの23の問題全部解説するまで帰れま23(21)
- 一般境界値問題とは?ヒルベルトの23の問題全部解説するまで帰れま23(20)
- 正則な変分問題の解は常に解析的?ヒルベルトの23の問題全部解説するまで帰れま23(19)
- 合同な多面体で空間を埋めろ?ヒルベルトの23の問題全部解説するまで帰れま23(18)
- 定符号の式を完全平方式で表すとは?ヒルベルトの23の問題全部解説するまで帰れま23(17)
- 代数曲線と曲面の位相の問題とは?ヒルベルトの23の問題全部解説するまで帰れま23(16)
- シューベルトの数え上げ計算とは?ヒルベルトの23の問題全部解説するまで帰れま23(15)
- 不変式系の有限性の証明とは?日本人が解決!ヒルベルトの23の問題全部解説するまで帰れま23(14)
- 7次方程式は2変数の関数で解ける?ヒルベルトの23の問題全部解説するまで帰れま23(13)
- 類体の構成問題とは?ヒルベルトの23の問題全部解説するまで帰れま23(12)
- 代数体上の二次形式の分類とは?ヒルベルトの23の問題全部解説するまで帰れま23(11)
- ディオファントス方程式に整数解があるか判別できる?ヒルベルトの23の問題全部解説するまで帰れま23(10)
- 数体の一般相互法則とは?ヒルベルトの23の問題全部解説するまで帰れま23(9)
- リーマン予想とは?ヒルベルトの23の問題全部解説するまで帰れま23(8)
- 種々の数の無理性と超越性とは?ヒルベルトの23の問題全部解説するまで帰れま23(7)
- 物理学の諸公理の数学的扱いとは?ヒルベルトの23の問題全部解説するまで帰れま23(6)
- 位相群がリー群となるための条件とは?ヒルベルトの23の問題全部解説するまで帰れま23(5)
- 二点間の最小距離は直線?ヒルベルトの23の問題全部解説するまで帰れま23(4)
- 等底・等高な2つの四面体の等積性とは?ヒルベルトの23の問題全部解説するまで帰れま23(3)
- 算術の公理間の整合性をわかりやすく解説!ヒルベルトの23の問題全部解説するまで帰れま23(2)
- 連続体仮説とは?ヒルベルトの23の問題全部解説するまで帰れま23(1)
- ミレニアム懸賞問題全部解説するまで帰れま7記事一覧!順番の意味も解説!
- バーチ・スウィンナートン=ダイアー予想とは?ミレニアム懸賞問題全部解説するまで帰れま7(7)
- ポアンカレ予想とは?ミレニアム懸賞問題全部解説するまで帰れま7(6)
- ホッジ予想とは?ミレニアム懸賞問題全部解説するまで帰れま7(5)
- ナビエ–ストークス方程式の解の存在と滑らかさとは?ミレニアム懸賞問題全部解説するまで帰れま7(4)
- P≠NP予想とは?ミレニアム懸賞問題全部解説するまで帰れま7(3)
- リーマン予想とは?ミレニアム懸賞問題全部解説するまで帰れま7(2)
- ヤン–ミルズ方程式と質量ギャップ問題とは?ミレニアム懸賞問題全部解説するまで帰れま7(1)
- プリヒタの素数円とは?描き方や歴史も解説!
- スライドパズルの解けない配置!サムロイドの14-15パズル
- オイラーの公式の中学生でもわかる証明!美しいvs美しくない!?
- 【図解】円周率はなぜ終わらない?無理数の証明!中学生でもわかる!
- ハノイの塔64枚で世界滅亡?漸化式&最短手数・元ネタと歴史を解説!
- フィールズ賞2022年の受賞者の理由・業績を紹介!
- フィールズ賞2022年の候補を大胆予想!女性、日本人候補は?
- 素数に1は入る?これだけの理由があった!
- 四色問題の立体版はなぜ考えられない?立体は2色で塗れる?
- ケンプ鎖を簡単に解説!ケンプの失敗と功績は?【しくじり科学者4】
- 非ユークリッド幾何学の歴史を解説!-クラインモデルの解説!
- 公理と公準の違いを詳しく解説!
- 結び目理論とDNAの関係について解説!-面白い応用例・遊び
- ネウシス作図!定規・コンパスのみで角の三等分【動画】-作図可能な具体例
- P≠NP予想 証明への歴史
- 非推移的サイコロ3種!ジッヒャーマンダイス-確率論のサイコロ
- 3次元の接吻数が12であることを図で証明!接吻数論争の歴史
- ブルバキのモデル!実在のブルバキ将軍の生涯を解説!ブルバキに娘がいた?
- 4色問題(四色問題)の反例が発見された?!
- 点予想 証明の歴史-フェルマーの最終定理との関係
- 解の公式の歴史!作った人・誰が発見者?解の公式の呪い?
- ファジィ理論の歴史
- 角の3等分の方法が発見された?!
- リーマン予想 証明への歴史
- ポアンカレ予想 証明の歴史
- フェルマーの最終定理 証明の歴史
- ケプラー予想 証明の歴史
- 四色問題の証明の歴史!地図と150年をめぐる大冒険!コンピュータによる証明で波乱も?
- 数学者たちのエイプリルフール
- ガウス『数学日記』における発見と謎
考察
・不幸が続いたのは偶然か?
これは偶然と呼ぶほかないが、社旗情勢も一枚かんでいるのかもしれない。病気が治るようになるには時間がかかり、また、フランスの不安定な革命期の情勢による不幸、と呼ぶことができないでもない。
・虚数の発展
方程式の解の公式を見つける過程で、どうしても導入が必要だったのが虚数の概念である。これは相当受け入れがたかったようだが、方程式の探求が虚数の理解に貢献したことは言うまでもない。
虚数は2次方程式の解としても出てくるが、この時は「答えとしてあり得ないので、考えなくてよい」、という解釈が主流だったようである。