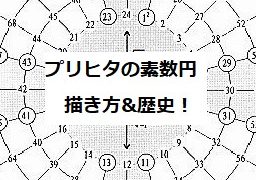
数学 プリヒタの素数円とは？描き方や歴史も解説！
素数を図示するのに使われる表現方法のうちの一つである『プリヒタの素数円』について解説していきます。また、描き方も解説しています。プリヒタの素数円（Prime Number Circle）とはプリヒタの素数円とは、素数を図的に表す方法の一つで...
数学
数学 
ゲーム スライドパズルの解けない配置！サムロイドの14-15パズル
スライドパズルは、かつてたくさんのゲーマーを熱中させた「解けない配置」が存在します。ここではその配置を持つパズルについて解説していきます。このパズルはブラウザ上でできますので、本当にできないパターンであることを確認することができます。スライ...
数学 オイラーの公式の中学生でもわかる証明！美しいvs美しくない！？
美しい数式として知られるオイラーの公式の簡単な証明を解説していきます。なおこの公式は、オイラーの等式、オイラーの恒等式、という呼ばれ方もしますが、ここではオイラーの公式で統一します。オイラーの公式の証明！指数関数の定義から計算するとわかりや...
数学 【図解】円周率はなぜ終わらない？無理数の証明！中学生でもわかる！
円周率πは、円にかかわる無理数として知られています。円周率はなぜ終わらないのかにかかわるのが無理数性の証明です。ここでは、π無理数であることの証明を簡単に行います。中学生でもわかるように図形的に解説します。円周率はなぜ終わらない？無理数であ...
数学 ハノイの塔64枚で世界滅亡？漸化式&最短手数・歴史を解説！
ハノイの塔は、数学的にもいろいろと考察されているパズルです。前回は、解き方のコツについて解説しました。ここでは、漸化式や最短手数などの数学的要素、歴史についてを解説します。64枚の時は世界滅亡というキーワードについても解説します。ハノイの塔...
数学 フィールズ賞2022年の受賞者の理由・業績を紹介!
フィールズ賞が四年ぶりに開催され、受賞者が発表されました。ここでは、彼らの受賞理由を解説するとともに、業績やプロフィールを紹介します。なお、専門分野に立ち入って解説するのは難しいため、概要のみとなります。こちらで予想もしていました：フィール...
数学 フィールズ賞2022年の候補を大胆予想!女性、日本人候補は?
2022年は4年ぶりのフィールズ賞の年となっております。フィールズ賞の候補を独断と偏見により予想してみました。すべての場合において業績の内容は専門的過ぎて触れることができませんが、年齢や受賞暦、共同研究などから候補を予想しました。結果はこち...
数学 素数に１は入る？これだけの理由があった！
素数について学ぶと、１は素数に含めないということも同時に学ぶが、これに納得できないという感情も抱くこともあるだろう。また、今日でも１が素数に入るというような表現を見かけることがある。これについて、いくつもの方法で解説する。なぜか１を素数に含...
数学 四色問題の立体版はなぜ考えられない?立体は2色で塗れる?
四色問題は平面幾何やグラフ理論の面白い問題であるが、これを立体にしたらどうなるか、というのも実は考案されている。しかし、あまり問題にはされない。その理由を詳しく解説する。四色問題の立体版の歴史立体版は、意外にも平面のオリジナルの四色問題が提...
人物伝 ケンプ鎖を簡単に解説!ケンプの失敗と功績は?【しくじり科学者4】
四色問題の証明として、一度はただしいと認められたケンプ鎖の内容について解説する。また、ケンプの功績についても解説する。ケンプ鎖の解説ケンプ鎖の証明の前知識として、いかが必要である。・5色ないとぬれない地図があるとすると、その地図のうちもっと...
数学 非ユークリッド幾何学の歴史を解説！-クラインモデルの解説！
ユークリッドの原論が出版されて以来の注目の的であった「平行線公準」。これを公準ではなく定理なのではないかと考え、ほかの公準から証明しようとする試みは、数世紀も続いた。しかしながら、別の幾何学が生まれるという意外な結末を迎えた。非ユークリッド...
数学 公理と公準の違いを詳しく解説！
公理と公準はユークリッド原論ででてくることばであり、どちらも「証明なしで正しいとみなす事柄」であるので違いがわかりにくい。この記事では、この言葉のちがいや歴史をわかりやすくまとめた。公理と公準の違い以下のように、いくつかの観点から解説が可能...
数学 結び目理論とDNAの関係について解説！-面白い応用例・遊び
結び目理論は数学の研究分野であるが、二重螺旋の構造をもつDNAの研究にも役立てられている。これと歴史について解説する。また、面白い意応用例や遊びを紹介する。結び目理論とDNAの関係DNAは小さな細胞核のなかにとても長い線が収納されており、絡...
数学 ネウシス作図！定規・コンパスのみで角の三等分【動画】-作図可能な具体例
ネウシス作図という「グレーゾーンの作図」をすれば、角の三等分は不可能ではないことが知られている。ここでは、ネウシス作図の実例として角の三等分について解説する。三等分になっていることの証明も解説する。関連：角の3等分の方法が発見された？！ネウ...
数学 P≠NP予想 証明への歴史
数学、あるいは計算機科学の未解決問題であるP≠NP予想の歴史。予想の年表1950まで チューリングマシン1965 ハートマニス、スターンズ、計算複雑さの論文、時間内に解けるかどうかの枠組を議論指数関数的時間がかかる問題が発見されはじめる。1...
数学 非推移的サイコロ3種!ジッヒャーマンダイス-確率論のサイコロ
確率論ではサイコロが例題として挙げられることが多いが、中にはそれらの応用として面白い性質をもつものが登場するる。有名な非推移サイコロをはじめとしてそれらをまとめた。また、その他のサイコロを題材にした不可能な問題も紹介している。非推移サイコロ...
数学 3次元の接吻数が12であることを図で証明！接吻数論争の歴史
3次元の接吻数（kissing number）は12であることが知られているが、3次元の接吻数にはニュートンが絡んだ論争があった。その歴史と、厳密ではないが簡単な証明を解説する。ざっくりとした証明図入りでまず2次元で解説する。これはイメージ...
人物伝 ブルバキのモデル！実在のブルバキ将軍の生涯を解説！ブルバキに娘がいた？
匿名の数学者たちの集団のハンドルネームである二コラ・ブルバキには、モデルといわれている同名の将軍がいる。その生涯について詳しく解説する。実在のブルバキ将軍の生涯シャルル・ドニ・ソテル・ブルバキ （1816～1897）フランスの軍人。ブルバキ...
数学 4色問題（四色問題）の反例が発見された？！
四色問題は、長い間解決されなかった難問であるが、その過程で、反例と思われるものが提出されたことがある。それを年表でまとめた。 なお、証明方法が間違っていることを示すものであって、四色問題そのものの反例ではない。よって、すべて4色あればぬれる...
数学 点予想 証明の歴史－フェルマーの最終定理との関係
解けそうで解けない難問の一つだった数学の問題に「点予想」がある。サイモン・シンの名著「フェルマーの最終定理」に載っていることで興味を持った人も多いかもしれない。 この問題がたどった歴史については当該図書には載っていないが、以下のような年表に...