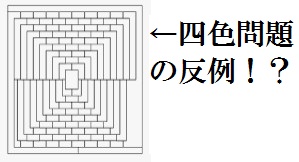
四色問題は、長い間解決されなかった難問であるが、その過程で、反例と思われるものが提出されたことがある。それを年表でまとめた。
なお、証明方法が間違っていることを示すものであって、四色問題そのものの反例ではない。よって、すべて4色あればぬれる。暇な人は塗ってみよう。
四色問題の反例 年表
1879:ケンプ、「ケンプ鎖」の発想を使って四色問題を解決したかに思われたが・・・ケンプ鎖を使えば、一色余らせることができ、4色で塗れる。
ケンプ:
ケンプ鎖の考え方をつかえば、どんな地図でも4色で塗り分けられる。QED
ヒーウッドの反例
1889:ヒーウッド(ヘイウッド)の反例・・・ケンプ鎖を適用しても色が余らない例がみつかった。

ヒーウッド:
ケンプ鎖が交差してしまうと、隣あった国が同じ色になってしまう例がある。ケンプの証明は誤り。
ド・ラ・ヴァレ・プーサンの反例
1896:ド・ラ・ヴァレ・プーサンの反例・・・国数は13で、ケンプ鎖の方法に対する最小の反例となっている。

ヒーウッドの地図よりも国数の少ない地図はつくれる。
エレーラの反例
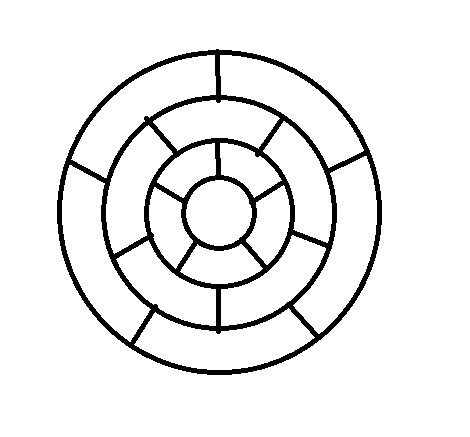
1921:エレーラの反例・・・対照的な美しい形をしている。
ガードナーと反例(エイプリルフール)
1975:ガードナーの反例・・・これはエイプリルフールだったが、本当だと勘違いした読者から、「4色で塗れたぞ」との手紙が多数届いたという。この時はこれのほかにも面白いジョークを発表している。ジョークを読めばこれがエイプリルフールだともわかる。
引用:https://mathworld.wolfram.com/McGregorMap.html
ムーアの地図
1960代:ムーアの地図・・・塗るのが難しい配置を組み合わせていき、反例を作ろうとする試みが一方では研究されていた。将来的には、このような試みから反例がみつかるのではという見方もあった。しかし、これも4色で塗れる。
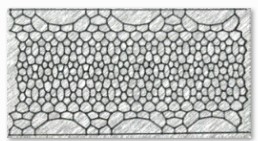
引用:四色問題、R・ウィルソン
ムーアの地図の塗り分けの答えは四色問題の新書などでカラーで載っている。
1970年代:最終的な4色問題の解決。反例は見つからないまま証明が完成した。
豆知識
・今でも数学者の研究室には、たまに四色問題の反例、つまり5色が必要な地図が送られてくることがあるそうである。しかし、4色で塗り分けられる。
おすすめ
- 素数の公式『ミルズの公式&ミルズ定数』定数をかけるだけで素数が?
- 四色問題の証明は美しくない?!批判と反論まとめ!実は美しい証明もあった!
- 正17角形の簡単な作図方法!10分でできる!定規とコンパスで描いてみよう
- 素数の公式『ウィランズの公式』解説!ウィルソンの定理との関係も!
- スメイルの問題全部解説するまで帰れま18記事一覧
- 微分同相写像とリー群モデルの関係とは?スメイルの問題全部解説するまで帰れま18(番外編3)
- 三次元球面は最小集合?スメイルの問題全部解説するまで帰れま18(番外編2)
- 平均値問題とは?スメイルの問題全部解説するまで帰れま18(番外編1)
- 人間と人工知能の知能の限界とは?スメイルの問題全部解説するまで帰れま18(18)
- 多項式を平均多項式時間で解くとは?スメイルの問題全部解説するまで帰れま18(17)
- ヤコビアン予想とは?スメイルの問題全部解説するまで帰れま18(16)
- ローレンツアトラクターの特性とは?スメイルの問題全部解説するまで帰れま18(14)
- 微分同相写像の中心化群とは?スメイルの問題全部解説するまで帰れま18(12)
- 1次元力学系は一般に双曲型?スメイルの問題全部解説するまで帰れま18(11)
- Pughの閉補題とは?日本の研究者も活躍!スメイルの問題全部解説するまで帰れま18(10)
- 線形計画問題とは?スメイルの問題全部解説するまで帰れま18(9)
- 経済学理論への力学の導入とは?スメイルの問題全部解説するまで帰れま18(8)
- 2-球面上の点の分布とは?スメイルの問題全部解説するまで帰れま18(7)
- 天体力学における相対平衡数の有限性とは?スメイルの問題全部解説するまで帰れま18(6)
- ディオファントス曲線の高さ境界とは?スメイルの問題全部解説するまで帰れま18(5)
- 1変数多項式の整数零点についてのτ予想とは?スメイルの問題全部解説するまで帰れま18(4)
- ヒルベルトの23の問題全部解説するまで帰れま23記事一覧
- ヒルベルトの24番目の問題とは?隠された謎とその内容に迫る!
- 変分法の研究の展開とは?ヒルベルトの23の問題全部解説するまで帰れま23(23)
- 保型関数による解析関数の一意化とは?ヒルベルトの23の問題全部解説するまで帰れま23(22)
- モノドロミー群をもつ線型微分方程式とは?ヒルベルトの23の問題全部解説するまで帰れま23(21)
- 一般境界値問題とは?ヒルベルトの23の問題全部解説するまで帰れま23(20)
- 正則な変分問題の解は常に解析的?ヒルベルトの23の問題全部解説するまで帰れま23(19)
- 合同な多面体で空間を埋めろ?ヒルベルトの23の問題全部解説するまで帰れま23(18)
- 定符号の式を完全平方式で表すとは?ヒルベルトの23の問題全部解説するまで帰れま23(17)
- 代数曲線と曲面の位相の問題とは?ヒルベルトの23の問題全部解説するまで帰れま23(16)
- シューベルトの数え上げ計算とは?ヒルベルトの23の問題全部解説するまで帰れま23(15)
- 不変式系の有限性の証明とは?日本人が解決!ヒルベルトの23の問題全部解説するまで帰れま23(14)
- 7次方程式は2変数の関数で解ける?ヒルベルトの23の問題全部解説するまで帰れま23(13)
- 類体の構成問題とは?ヒルベルトの23の問題全部解説するまで帰れま23(12)
- 代数体上の二次形式の分類とは?ヒルベルトの23の問題全部解説するまで帰れま23(11)
- ディオファントス方程式に整数解があるか判別できる?ヒルベルトの23の問題全部解説するまで帰れま23(10)
- 数体の一般相互法則とは?ヒルベルトの23の問題全部解説するまで帰れま23(9)
- リーマン予想とは?ヒルベルトの23の問題全部解説するまで帰れま23(8)
- 種々の数の無理性と超越性とは?ヒルベルトの23の問題全部解説するまで帰れま23(7)
- 物理学の諸公理の数学的扱いとは?ヒルベルトの23の問題全部解説するまで帰れま23(6)
- 位相群がリー群となるための条件とは?ヒルベルトの23の問題全部解説するまで帰れま23(5)
- 二点間の最小距離は直線?ヒルベルトの23の問題全部解説するまで帰れま23(4)
- 等底・等高な2つの四面体の等積性とは?ヒルベルトの23の問題全部解説するまで帰れま23(3)
- 算術の公理間の整合性をわかりやすく解説!ヒルベルトの23の問題全部解説するまで帰れま23(2)
- 連続体仮説とは?ヒルベルトの23の問題全部解説するまで帰れま23(1)
- ミレニアム懸賞問題全部解説するまで帰れま7記事一覧!順番の意味も解説!
- バーチ・スウィンナートン=ダイアー予想とは?ミレニアム懸賞問題全部解説するまで帰れま7(7)
- ポアンカレ予想とは?ミレニアム懸賞問題全部解説するまで帰れま7(6)
- ホッジ予想とは?ミレニアム懸賞問題全部解説するまで帰れま7(5)
- ナビエ–ストークス方程式の解の存在と滑らかさとは?ミレニアム懸賞問題全部解説するまで帰れま7(4)
- P≠NP予想とは?ミレニアム懸賞問題全部解説するまで帰れま7(3)
- リーマン予想とは?ミレニアム懸賞問題全部解説するまで帰れま7(2)
- ヤン–ミルズ方程式と質量ギャップ問題とは?ミレニアム懸賞問題全部解説するまで帰れま7(1)
- プリヒタの素数円とは?描き方や歴史も解説!
- スライドパズルの解けない配置!サムロイドの14-15パズル
- オイラーの公式の中学生でもわかる証明!美しいvs美しくない!?
- 【図解】円周率はなぜ終わらない?無理数の証明!中学生でもわかる!
- ハノイの塔64枚で世界滅亡?漸化式&最短手数・元ネタと歴史を解説!
- フィールズ賞2022年の受賞者の理由・業績を紹介!
- フィールズ賞2022年の候補を大胆予想!女性、日本人候補は?
- 素数に1は入る?これだけの理由があった!
- 四色問題の立体版はなぜ考えられない?立体は2色で塗れる?
- ケンプ鎖を簡単に解説!ケンプの失敗と功績は?【しくじり科学者4】
- 非ユークリッド幾何学の歴史を解説!-クラインモデルの解説!
- 公理と公準の違いを詳しく解説!
- 結び目理論とDNAの関係について解説!-面白い応用例・遊び
- ネウシス作図!定規・コンパスのみで角の三等分【動画】-作図可能な具体例
- P≠NP予想 証明への歴史
- 非推移的サイコロ3種!ジッヒャーマンダイス-確率論のサイコロ
- 3次元の接吻数が12であることを図で証明!接吻数論争の歴史
- ブルバキのモデル!実在のブルバキ将軍の生涯を解説!ブルバキに娘がいた?
- 4色問題(四色問題)の反例が発見された?!
- 点予想 証明の歴史-フェルマーの最終定理との関係
- 解の公式の歴史!作った人・誰が発見者?解の公式の呪い?
- ファジィ理論の歴史
- 角の3等分の方法が発見された?!
- リーマン予想 証明への歴史
- ポアンカレ予想 証明の歴史
- フェルマーの最終定理 証明の歴史
- ケプラー予想 証明の歴史
- 四色問題の証明の歴史!地図と150年をめぐる大冒険!コンピュータによる証明で波乱も?
- 数学者たちのエイプリルフール
- ガウス『数学日記』における発見と謎
考察
・コンピュータの証明の影響?
四色問題はコンピュータを使って証明されたので、「もしかしたらバグがあって、コンピュータが証明できなかった部分に反例が隠れているのでは」、という思いが、いまだに反例への想像をかきたてていると考えることもできる。
もっとも、コンピュータの証明も実際には簡素化されていき、コンピュータの性能の良さも発展したこととあいまって、その可能性はほとんど0に近いのが現状である。