点予想証明の歴史－フェルマーの最終定理との関係

　解けそうで解けない難問の一つだった数学の問題に「点予想」がある。サイモン・シンの名著「フェルマーの最終定理」に載っていることで興味を持った人も多いかもしれない。
　この問題がたどった歴史については当該図書には載っていないが、以下のような年表にまとめることができる。
→フェルマーの最終定理　証明の歴史

年表
1. 一応証明された
2. 簡単な証明
豆知識
おすすめ
考察

年表

1893：シルヴェスターが問題を提起する
1893頃：証明が発表される。しかし、この証明には不備があった。

一応証明された

1941： Melchiorによって、グラフ理論におけるオイラーの等式を元に証明。
1943：エルデシュ、同様の予想を述べる。
直後：エルデシュの予想もMelchiorによって同様に証明される。
1969：コクセターの証明。・・・より一般化された問題について証明する形で展予想を証明した。

簡単な証明

1986：ケリーが簡潔な証明を発見・・・これが「フェルマーの最終定理」に載っている証明である。これが最も簡単な証明として知られる。

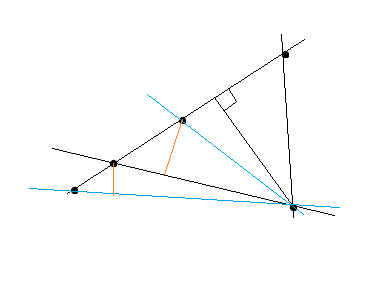
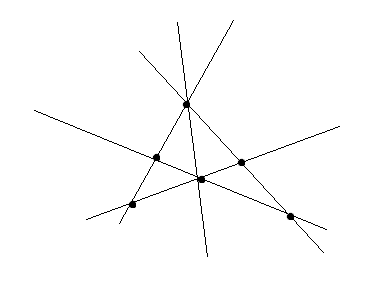
距離が最小の点を選んでも、3つの点があるとさらに最小の距離が見つかってしまい矛盾が生じる

平面上の直線と点の集合については、すべての点が一直線上にあるか、少なくとも一本は2点しか乗らない直線が存在する。
syllvester-gallaiの定理

これを別の言い方をしたのが点予想である。

1997：「フェルマーの最終定理」出版。この書物では「実は簡単に証明できた幾何学の問題」として、点予想を例に出して解説している。

たしかに、終わってみれば証明は簡単だったと感じられる歴史である。普通に証明するのに50年くらい、簡単な証明までは90年と少しの時間を要した。

豆知識

・エルデシュは幾何学への貢献が多くあるが、たくさんの予想を提出することで有名だった。この事例ではすでにある予想とかぶってしまったといえる。

考察

・アンドリューワイルズは点予想の証明を知っていたのか？
　　フェルマーの最終定理の謎を解き明かしたワイルズであるが、サイモン・シンの著作「フェルマーの最終定理」の内容を読む限り、ワイルズが知っていたとも、知らなかったとも取れるような書き方を、点予想についてしているのである。上述の通り、簡単に溶けた証明の例として述べられているが、ワイルズがこのことを知っていたとは限らない。

１．知らなかった説
最終的には、ワイルズは現代数学の全精力を集めて証明を完成させた。これは幾何学の問題というより、楕円方程式の分野である。対して点予想は幾何学の分野で、あるいはグラフ理論の分野で証明がなされたのであり、ワイルズがさんこうにしたとは考えにくいかもしれない。また、書物の中でサイモン・シンはワイルズに取材をしてインタビューをしているが、どうもその中では点予想には触れられていないようである。

２．知っていた説
ワイルズの数学者としての研究生活のうちで、一度は点予想について聞き及んでいたとしても不思議ではない。また、子の証明はフェルマーの最終定理前までに簡単な証明が得られているので、「簡単な証明が見つかった」というニュースが数学界に流れたとしても不思議ではない。

・簡易な証明の心理的な効果
数学はある問題について定理が得られたとしても、同じ問題をより簡単に証明することを追及するのが習慣として認められている。この問題についても、証明が提出されてから40年後に簡単なものにブラッシュアップされた。このような簡単な証明は、難しい問題に取り組む数学者の背中を押す効果があるのかもしれない。また、アマチュアにとっても「これくらいならできそうだ」と問題に挑戦する契機になる可能性はある。

年表

一応証明された

簡単な証明

豆知識

おすすめ

考察