四色問題の証明として、一度はただしいと認められたケンプ鎖の内容について解説する。また、ケンプの功績についても解説する。
ケンプ鎖の解説
ケンプ鎖の証明の前知識として、いかが必要である。
・5色ないとぬれない地図があるとすると、その地図のうちもっとも国が少ないものがある。これを最小反例という。
・最小反例には、四角形の国か五角形の国が含まれる。
ケンプ鎖の基本的なアイディアは、「色をあまらせることで、最小反例も4色で塗れてしまうということを示す」というものである。この考えは、四角形か五角形の国の周りでのみ立証できればOKわかっていた。
ケンプ鎖とは
ある国から、二色の色を選んでたどっていくと、鎖のような形状が得られる。これがケンプ鎖である。
したの図の赤と緑の国のつながりがケンプ鎖である。
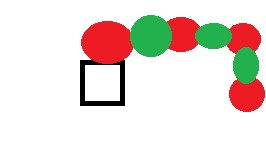
これは、鎖が途中で途切れている(枝分かれはあってよい)という場合か、鎖が四角形の国に戻ってくるかの二通りが考えられる。(下図)
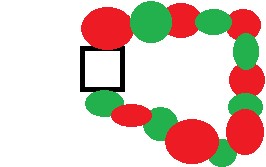
四角形の国について証明を解説する。
鎖が途切れているときは、赤と緑を入れ替えても他の国に影響を及ぼさないので、赤と緑を入れ替えることで四角形の周りの色を一色あまらせることができる。
鎖が輪になって四角形に戻ってくる場合は、赤と緑を入れ替えても意味はない。しかし、青と黄色に注目すると、この和によって青と黄色は途切れていることが確定するので、青と黄色の入れ替えをすることで、1色あまらせることができる。
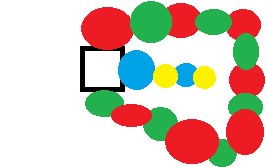
ケンプ鎖の間違い
五角形では場合わけがちょっとおおくなる。具体的には、五角形の底辺につながっている場合と、底辺ではないところにつながっている場合などである。(鎖が途切れている場合は、4角形の場合と同じである。)
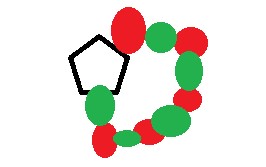
ケンプは、この場合もケンプ鎖で論証することで、証明を成し遂げたかに思われた。
しかし、五角形の場合はケンプ鎖で入れ替えをしようとすると同じ色が隣り合ってしまう場合があり、これが証明のあやまりであった。
ケンプの功績
研究者としての地位
アルフレッド・ブレイ・ケンプ(Alfred Bray Kempe)は、イギリス生まれの数学者である。

ケンプは18世紀末の数学者として著名な人物であった。今日、4色問題の証明に失敗した人という面でしか記憶されていないのは残念なことである。
リンク機構の開発
ケンプはリンク機構の開発に功績があることで知られている。数学的な問題をとくものもあるが、地図をなぞって作図するようなリンク機構をつくることに成功した。
なお、文献によってはスペルからの連想で「ケンペ」と名前を訳されていることがあるが、ただしいのは「ケンプ」なので気を付けよう。



