プリヒタの素数円とは？描き方や歴史も解説！

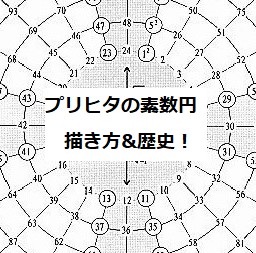
素数を図示するのに使われる表現方法のうちの一つである『プリヒタの素数円』について解説していきます。また、描き方も解説しています。

プリヒタの素数円（Prime Number Circle）とは

プリヒタの素数円とは、素数を図的に表す方法の一つです。英語では”Prime Number Circle(PNC)”などとも呼ばれるようです。

自然数を円周の上に並べていくと、図のように素数が配置される場所がきれいに決まった直線の上に並ぶ、というものです。

法則船がわからない素数がかなり規則正しく並んで見えるので、図示の方法として有名です。

これは日本語版のWikipedia「素数」のページにも載っているので、気になった人も多いのではないでしょうか。

以下では、プリヒタの素数円の書き方を解説していきます。

プリヒタの素数円を描くには、以下の手順に従っていきます。

まずは24方向に延びる直線を原点から引いていきます。

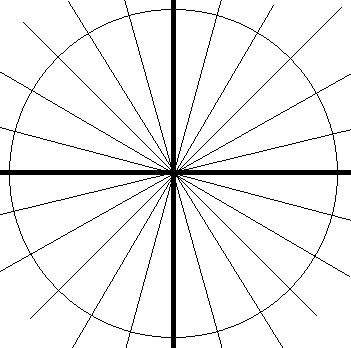
また、同心円状に数字を配置するために、円もいくつか書いておくと見やすくなります。

ここから数字を振っていきます。

右上のエリアの一番上の斜め線から1、２、３・・・と時計回りに置いていきます。（以下の図では一部の自然数を省略しています。）

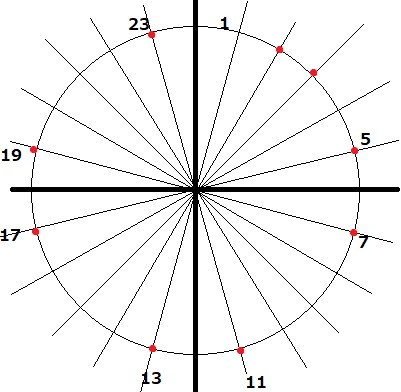
そして、数字が素数であれば、わかりやすくマークしておきます。上の図では赤くした点が素数に相当しています。

ただし、唯一の偶素数である2と最初の奇素数3はマークしないでおくことも多いようです。

上のプロセスを、24個おきに別の大きな円を広げてその上に置いていく、という形で繰り返します。

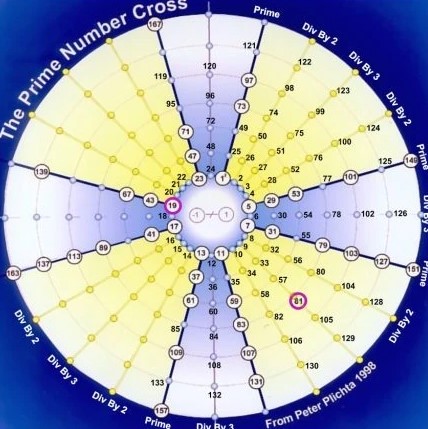
すると、素数がちょうど末広がりの十字架を描くような位置に収まっていることがわかります。

具体的には、

の4か所です。

ただし、上でも書いたように２、３はマークされておらず、仮にこれらをマークするとそこだけ十字架からは外れた位置に存在します。

プリヒタの素数円は「対称的な決まった範囲に素数が集まる」という数学的な面白さがあります。

形的にも素数の位置が直観的にわかりやすいです。

また、これがテンプル騎士団が使用していた十字架と似たような形を描くので、神秘的な美しさがある、ということのようです。

プリヒタの素数円は銅発見されたのでしょうか？

これは、ピーター・プリヒタというドイツの化学者によって発見されましたが、それ以前から知られていたという説もあるようです。

具体的な書籍としては、プリヒタによる1991年の書籍『Das Primzahlkreuz I（素数の十字架 I）』を通じて広く知られるようになったようです。

素数の図示をする方法でオリジナルなものを考えるのも面白そうです。