今回は、数の不思議に満ちた「素数の公式」の中でもちょっと変わり種、ミルズの公式とミルズ定数についてご紹介します。
素数といえば、「2, 3, 5, 7, 11, 13, 17…」と続く、割り切れない数字たちのこと。数学の世界でも、暗号技術など現実世界でも大活躍の存在です。
でも、実はそんな素数に「公式」があるってご存じでしたか?
この記事では、
- 素数を“全部”出すわけじゃないけど“結果が全部素数”になる不思議な公式
- ミルズ定数ってなに?
- 公式って使えるの?使えないの?
そんな疑問に、わかりやすく答えていきます!
🔍 素数の公式には別種もある!
まず、「素数の公式」と聞いて思い浮かぶのは、例えば「n を入れたら n 番目の素数が出てくる公式」みたいなやつですよね。
有名なのは、前回紹介したウィランズの公式や、マチャセビッチの多項式など。
ただしそれらは、
- 計算量が重すぎて現実的じゃない
- そもそも式自体がめちゃくちゃ複雑
という“数学者向け”の式でした。
それに対して今回紹介するのは、「全ての素数が出るわけじゃないけど、出てくる数は全部素数!」という、ちょっと珍しい公式です。
その代表が…
🔷 ミルズの公式(Mills’ Formula)
そしてそこに出てくる謎の数字が…
🔷 ミルズ定数(Mills’ Constant)
✨ ミルズ定数とミルズの公式
💎 ミルズ定数とは?
ミルズ定数(Mills’ constant)とは、1952年に数学者ウィリアム・ミルズ(William Mills)が理論的にその存在を示した定数です。
その性質はズバリ!
ある定数 A が存在して、⌊A^(3^n)⌋
(Aを3^n乗し、整数部分を取ったとき)の結果がすべて素数になる!
…っていう、不思議な話。
たとえば、Aがその“魔法の定数”なら:
- n=1:⌊A^3⌋=2
- n=2:⌊A^27⌋=11
- n=3:⌊A^81⌋=1361
となり、結果はすべて素数!
🧮 じゃあそのミルズ定数 A の値は?
ここが面白いところなんですが…
実は 正確な値は分かりません。
というのも、この「ミルズ定数」は、素数の分布に関する深い理論(たとえばリーマン予想)に依存していて、
- リーマン予想が正しいなら存在は証明できる
- けど、正確な値はわからない
という、存在はわかってるけど、見えない幻の定数なのです。
一応、近似値は次のように求められています:
A≈1.3063778838630806904686144926…
でも、これは「リーマン予想が正しいと仮定して」計算された値です。
🧪 ミルズの公式とは?
では、ミルズの定理とミルズ定数を組み合わせてできる「ミルズの公式」を見てみましょう。
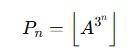
ミルズの公式(Mills’ Formula):
Pn=⌊A^3^n⌋
ここで、
- A:ミルズ定数
- n:正の整数
- Pn:生成される素数
この式に n=1,2,3,… と順番に入れていくと、素数だけが出てくる!
例:
| n | 式の中身 ⌊A3n⌋ | 結果 |
|---|---|---|
| 1 | ⌊A^3⌋= 2 | 素数 ✅ |
| 2 | ⌊A^27⌋ = 11 | 素数 ✅ |
| 3 | ⌊A^81⌋= 1361 | 素数 ✅ |
…となります。
この不思議な公式、まるで「A をどんどんべき乗して切り捨てれば素数になる魔法」のよう!
🚫 実用的ではない?
さて、ここまで聞いて「え、これすごくない?素数ジェネレーターじゃん!」と思った方もいるかもしれません。
ですが…残念ながら、実用性はほぼゼロです😅
理由1:A の正確な値がわからない
- 近似値しかない
- ほんの少しでもズレてたら、床関数を取ったときに違う数(=素数じゃない)になってしまう
理由2:指数がでかすぎる
- A^3^nは、n がちょっと大きくなるだけで超巨大な数になります
- たとえば n=4 なら、3^4=81、そのべき乗 → 普通のPCでは無理ゲー
理由3:素数が順番に全部出るわけじゃない
- この公式で出てくるのは「ある特定の素数列」だけ
- すべての素数をカバーできるわけではない
💡 それでもロマンはある!
実用性はないけど、ミルズの公式はやっぱり面白い。
- 定数 × 指数で「素数だけ」が出てくる
- 存在証明だけで成り立つ、純粋数学の美しさ
- リーマン予想と絡む、深すぎる背景
こういう「不思議だけど使えない公式」にこそ、数学のロマンが詰まってるのかもしれませんね。
🧭 まとめ:ミルズの公式って何だったの?
✅ 本文の要点まとめ
- 素数を“全部”出すわけではないが、“結果が全部素数になる”公式がある
- ミルズ定数 AAA は、存在が証明されているが正確な値は不明(リーマン予想に依存)
- ミルズの公式:
pn=⌊A^3^n⌋で、結果はすべて素数! - ただし、実用性は低い(定数の不明確さ・巨大計算・素数の網羅性が低い)
- それでも「数学の美しいアイデア」として価値がある
数学の世界には、ウィランズの公式、マチャセビッチの多項式、そして今回紹介したミルズの公式のように、「発見したけど使えない」ロマンあふれる式がたくさんあります。
こういった公式を通して、「素数の奥深さ」や「数学の面白さ」に少しでも興味を持ってもらえたらうれしいです!