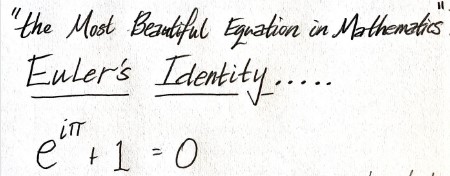美しい数式として知られるオイラーの公式の簡単な証明を解説していきます。なおこの公式は、オイラーの等式、オイラーの恒等式、という呼ばれ方もしますが、ここではオイラーの公式で統一します。
オイラーの公式の証明!指数関数の定義から計算するとわかりやすい
オイラーの公式の証明には、サインとコサインのテイラー展開を使い、式を展開していって等しいことを示すという方法が使えます。これは有名な方法ですが、もう少し簡単に証明してみましょう。
ネイピア数eを使った指数関数e^xあるいはexp(x)の定義は、以下のようなかっこ内の数式の累乗するものになっています。
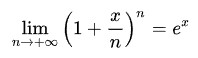
ここでx=1のときはネイピア数eの定義そのものになっているので、確かに上の定義が正しいことがわかります。
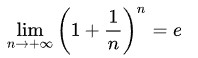
では、複素数に適用したときはどうなるでしょうか?
これは形自体は何も変わらずに、以下のようになります。zには、複素数が入ります。
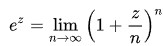
ということは、e^πiというのはz=πiのときということになるので、式の右辺は以下のように書けます。
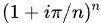
複素数に適用し、e^πiの形になるようにπiが代入できたので、定義に従って、Nを増やしていった場合どうなるかを調べてみましょう。Nが無限大になったときが、e^πiの値、ということになります。
N=1のときは簡単ですね、かっこは一つだけ、累乗の指数も1なので、そのまま(1+πi)です。これを複素平面に描くと、図の位置になります。
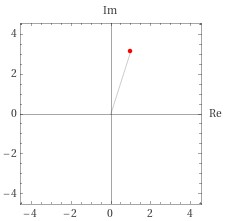
N=2の時は、かっこを展開して計算します。こちらも複素平面に描くと、図の位置になります。ここにきて、実数部分がマイナスになりました。
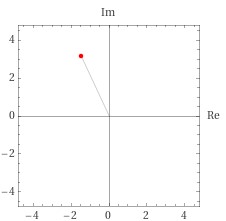
N=10まで飛ばすとどうなるでしょうか?こうすると、虚数部分は0になっていき、実数部分はかなり-1に近づいていることがわかります。
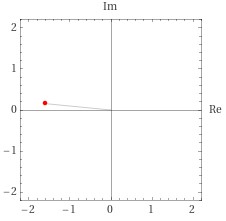
N=100では、もうほぼ-1になっていますね。
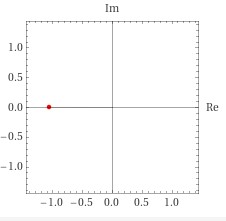
こうすることで、e^πi=-1ということが証明できました。あとは-1を移動すれば、
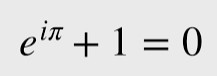
となり、オイラーの公式が得られます。
オイラーの公式は美しい?美しくない?
「世界一美しい数式」と呼ばれることも多いです。これはなぜかというと、
- 自然対数の底 e
- 円周率 π
- 虚数単位 i
- 単位元 1
- 零元 0
という数学の基本的な定数が一堂に会しているから、というのがその理由です。
たしかに、ここまできれいにそろっているのは珍しいですね。
美しい派の意見
美しいと思う人には、多くの数学者などが含まれます。有名なところでは、ガウスが以下のような言葉を残しています。
学生がこの数式を見て一目でその素晴らしさに気づくことができなければ、その人は決して一級の数学者にはなれない。
また、物理学者のリチャードファインマンは、よほど感動したらしく、この数式を大きくノートに書き記して、解説をくわえています。
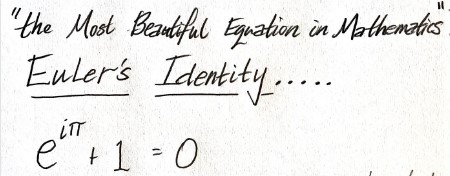
美しくないと思う人もいる?
なかには、美しくない、あるいは美しさが不十分であると感じる人もいるようです。
そうした人たちは、円周率ではなく半径と円周との比率(τ=6.28・・・で表現されることが多い。)を使うことで、もっとシンプルになると主張しています。
まとめ
- オイラーの公式は、自然対数の底の定義を使ってNを増やしていくことで、視覚的なかんたんな証明ができる。
- 美しいと思う人には、ガウスやファインマンなどがいる。
- 美しくないと思う人には、τを使ってよりシンプルにしようとする人もいる。
今後もこの数式を超える美しさにはちょっとお目にかかれなさそうですね。