数学の根幹をなす素数には、いくつものトピックがあります。
今回はそんな中でも、「素数の公式」と呼ばれるちょっと変わったやつを紹介します。その名も…
🔷 ウィランズの公式(Willans’ formula)
え、素数に公式なんてあるの!?
って思った方。実は、「素数には公式がない」ってよく言われているのに、こういう公式も存在するんです。でもちょっと複雑で非効率…。
この記事では、ウィランズの公式とは何なのか、素数に「公式がない」と言われる理由、そしてウィルソンの定理との深〜い関係もわかりやすく解説していきます!
「素数の公式はない」ってどういうこと?
まず、よく言われるこの言葉。
「素数には公式がない」
これは一体どういう意味なんでしょう?
実は、これはちょっと誤解を招きやすい言い方なんです。正確には、
「素数だけを次々に生成するような、シンプルで効率的な公式は存在しない」
というのが本当の意味です。
たとえば、2, 3, 5, 7, 11…って感じで、1つの数式から次々と素数だけを出してくれるような魔法の公式があったら、みんな使いたくなりますよね。
でも、そんなうまい話はないんです。
なぜなら、素数は「間隔」がランダムっぽくて法則性が見えにくいから。
でも、「非効率でもいいなら、素数を見つける公式はいくつかある」のです!
では登場!ウィランズの公式とは?
さあ、ここで満を持して登場するのが「ウィランズの公式」です。
この公式、なんとn番目の素数を数式で表せるという、めちゃくちゃ夢のあるやつなんです。
🔢 ウィランズの公式(ざっくり版)
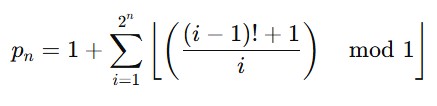
…え?
いきなり数式が爆誕してびっくりした?大丈夫、解説します!
この式の中身はこうです:
- iを 1 から 2^n まで増やしていく(つまり、かなりの数のループ)
- (i−1)!+1 を i で割る
- その「割り切れたかどうか」をチェックする
- 割り切れなかったら「1」、割り切れたら「0」を加算する
- そうして出てきた数に「1」を足すと、n番目の素数が出てくる!
🎩 なにがすごいの?
- 入力が「n」(素数の番号)だけ
- 出力が「n番目の素数」だけ
- 無駄な数を挟まない(2, 3, 5, 7, 11…と直接出る)
つまり、まさに素数専用マシンみたいな式!
…ただし計算量がバカ重い。
2^n 回もループを回す上に、毎回階乗の計算をしなきゃいけないので、nがちょっと大きくなるとPCが泣きます(人間も泣きます)。
ウィルソンの定理との関係は?
このウィランズの公式、ウィルソンの定理がベースになっています。
📜 ウィルソンの定理とは?
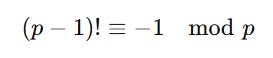
この定理の意味はこう:
もし p が素数なら、(p−1)! + 1 は p で割り切れる。
逆に言えば、
もし (p−1)! + 1 が p で割り切れるなら、p は素数。
これってすごくないですか?
素数かどうかを、「階乗を使って調べる」という超変わり種の方法なんです。
🤝 ウィランズ公式 × ウィルソン定理
ウィランズの公式は、このウィルソンの定理を利用して、次のような発想でできています。
- 「i」が素数かどうかを調べるには、ウィルソンの定理を使えばいい!
- つまり、(i−1)!+1が i で割り切れるかどうかをチェック!
- それを順番に調べて、素数だったものをカウント
- n個見つかったところで、それが「n番目の素数」!
つまりウィランズの公式は、「ウィルソンの定理を片っ端から試して素数を数える」という、超ゴリ押し系・物量タイプの公式だったんです!
じゃあ使えないの?ウィランズ公式の存在意義
「非効率なら意味ないじゃん」と思った人もいるかもしれません。
でも、実はそうでもないんです。
💡 意味があるポイント
- 「公式として素数だけを出す」ことができる
→ 数学的にはとても面白い構造! - シンプルで構造がわかりやすい
→ プログラムにもできるし、教育的価値がある - 理論的には“素数だけを生み出す公式”の例として貴重
ただし実用性はゼロに近いです(笑)
でも、「素数には公式がない」は、厳密には正しくないと教えてくれる公式ですね。
🎯 まとめ:ウィランズの公式って何だったの?
最後に、今日の内容をざっくり振り返り!
✅ 本文の要約(箇条書き)
- 「素数には公式がない」と言われるのは「効率的な公式がない」という意味
- 実際には、素数を出すことができる数式はいくつか存在する
- 「ウィランズの公式」は、n番目の素数を直接計算できる珍しい公式
- ウィランズの公式は「ウィルソンの定理」に基づいて構成されている
- 計算量が非常に大きいため、実用性は低いが理論的には面白い
- 「素数の構造」や「数学の奥深さ」を感じられる好例
🧠 最後にひとこと
ウィランズの公式は「非効率だけど夢がある」数学のロマン。
普段はあまり意識しないけど、こういう“ひねくれたアプローチ”から見ると、数学の世界って意外とポップで面白いんです。
もしこの記事でちょっとでも「数学って意外とおもしろいかも」と思ったら、あなたも立派な“数式探検隊”の仲間入りかもしれません!



