ピタゴラスの定理は数学のなかで最も有名な定理といってもよく、有名な人物が証明を提供している。その数は膨大な数になるが、そのうち有名なものを解説した。この中には、アインシュタイン、ガーフィールド大統領などが含まれる。
アインシュタインの証明
アインシュタインの証明は、ひとつの直角三角形を垂線によって二つに分解することで、相似比によってピタゴラスの定理を導くものである。
まず、図のように垂線をひくと、元の三角形と内部の二つの三角形は互いに相似形になる。このとき、辺どうしの対応から、
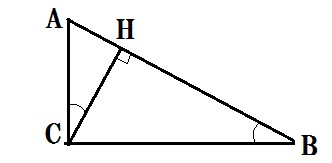
BC/AB=BH/BC かつ AC/AB=AH/AC
これらを整理すると BC^2=ABBH かつ AC^2=ABAH
この二つの式を足して、ABでくくると BC^2+AC^2=AB(AH+BH)
AH+BHは結局もとの三角形の斜辺ABなので
BC^2+AC^2=AB^2
となって。ピタゴラスの定理が成り立つ。
このアインシュタインによる証明は、10代のときに彼が自力で考え出した証明とも言われており、実際に彼の伝記などでも言及されることが多い。アインシュタインいわく、この発見が自身の人生に影響を与えたともいっている。
ガーフィールド大統領の証明
ガーフィールド大統領は、まだ議員だった時代に独自の証明を発表した。これは正方形ではなく台形をもちいるもので、証明もわかりやすい。

図のように二つのおなじ直角三角形を用意し、対角線のように線を引く。この結果全体が台形になる。
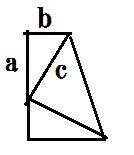
台形の面積の公式から全体は
1/2×(a+b)^2
なおかつ直角三角形が二つに二等辺三角形一つの面積を足すと
ab/2+ab/2+(c^2)/2
この二つは等しいので統合で結んで整理すると a^2+b^2=c^2
ガーフィールド大統領は暗殺された大統領としても知られている。でも、「ピタゴラスの定理の呪い」という都市伝説はないようである。
ダヴィンチの証明
いかではわかりやすいように直角二等辺三角形を使っているが、本筋は変わらない。
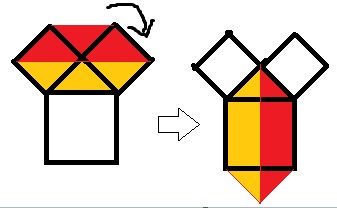
この三角形の各辺に接するように正方形をおいて、その上の部分を含めた領域を塗る。真ん中の上下の三角形がなければ、領域は二つの小さな正方形の面積のみとなる。
次にこれを90度回転させると、したの正方形と部分的に重なり、上下に三角形ができる。上下の三角形がなければ、領域は大きな正方形の面積のみとなる。
この変換からわかるように、小さな四角形の面積二つが、大きな正方形に等しいことがわかるので、ピタゴラスの定理がなりたつ。
ピタゴラスの定理の証明は100通りある?
ピタゴラスの証明はいろいろなひとが独自の証明を出しており、予測候補に100通りと出るくらいである。
実際の数はどうなのかというと、とうに100通りを超えている。たとえば以下のページなどはまとめたサイトである。
これらの証明をすべて理解したうえで、自分なりのあたらしい証明を考えるのも面白い試みだと思われる。



