こんにちは!
ヒルベルトの23の問題を1問ずつ解説していくシリーズ、今回は第13問に突入です!
今回のテーマは……
🧠「7次方程式の解は、2変数の関数で表現できるのか?」
えっ、それ何がすごいの?って思った方、ご安心ください。
この記事では、「なぜ7次なのか?」「2変数って何の話?」「結局この問題は解けたのか?」を、しっかり分かりやすく解説します!
■ まず、7次方程式ってなに?
数式で書くとこういう形です👇
x^7+a6x^6+⋯+a1x+a0=0
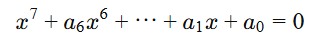
この「7次方程式」をどう解くか、というのがテーマなんですが、
ここで注目するのは「式の係数」や「解き方」の“関数としての表現”です。
■ なぜ「7次」なのか? 5次や6次はどうしたの?
ここでなぜ7次に注目しているのかを解説していきます。
● 有名なアーベル・ルフィニの定理
中学や高校で「2次方程式の解の公式」を学んだことはありますよね?
実は、3次や4次にも「解の公式」はあるんです。でもそれは、
✖「四則演算と根号だけ」でできるのは4次まで!
それ以上、つまり5次や6次、7次になると「公式による解法」がないのです。
アーベル・ルフィニの定理。
数学をかじったことがある人なら、5次方程式以降には解の公式がない、というのは一度は聞いたことがあると思います。
● じゃあこの問題、何を問うてるの?
5次以上が「根号と四則演算」で解けないのは知ってる。
でもヒルベルトが第13問で問うたのは、こういう方向の問題でした:
「7次方程式の解は、たった2つの変数を使った関数だけで書ける?」
普通の「代数的な解の公式」とは違って、「関数としての解の表現(しかも変数の数に制限あり)」という視点が加わっているんです!
■ なぜ「2変数」にこだわるのか?
数学では、「方程式の解を表すのに必要な変数の数=関数の次元」として考える視点があります。
- 6次方程式の解は、「2変数」では表せない(3変数以上が必要)ことが判明していた
- でも、7次方程式はもしかしたら2変数でいけるかも?という希望があった!
これ、ちょっと不思議ですよね?
実際、7次方程式の対称群 S7には、ある構造的な性質があって、
6次よりも「関数としての単純さ」がある…という深い話なんです。
■ 解決までの道のり
● 古典から現代へつながる問い
ヒルベルトがこの問題を出した1900年当時、まだ「関数の複雑さ」や「必要な変数の数」を厳密に測る方法はありませんでした。
でもその後、この問いは以下の分野へと発展していきます:
- 多変数関数論
- 代数的関数体の理論
- 多様体(高次元空間)の幾何学
● ヴェイユの突破(1927年)
フランスの大数学者アンドレ・ヴェイユが1927年に示したのが、以下の結果:
7次方程式の解は、2変数の代数関数で表現できる!
つまり、「ヒルベルト第13問」は部分的に肯定されたということになります!
■ さらなる飛躍:コルモゴロフ・アーノルドの定理(1957年)
1957年、ロシアの若き数学者ウラジミール・アーノルドがこの問題に革命をもたらします。
彼の師匠であるアンドレイ・コルモゴロフとの共同研究で生まれたのが…
🔹 コルモゴロフ=アーノルドの表現定理
これは簡単に言えば:
「任意の連続関数(特に方程式の解)も、2変数の連続関数を合成すれば表現できる」
というもので、ヒルベルト第13問の本質を完全に肯定的に解決したと評価されるようになります!
■ それでも「完全解決ではない」理由
✅ なぜ「部分的解決」扱い?
アーノルドの成果は確かにすごいですが、「連続関数での表現」によるものであり、
- 代数的関数
- 解析的関数(実解析や複素解析)
など、より厳しい条件での表現が可能かどうかは、未解決な側面が残っています。
だから数学界では、ヒルベルト第13問は「実質的に解決されたが、厳密には部分的解決」とされているのです。
■ 第13問が数学に与えた影響
● 1. 「解の複雑さ」を次元で測る発想
この問題を通じて、数学者たちは「解を表すのに必要なパラメーターの数」という視点を得ました。
これが後の:
- 多変数関数論
- 多様体の理論
- 数学的構造のミニマル表現
につながっていきます。
● 2. 多様体理論・代数幾何への橋渡し
「2変数関数で解けるのか?」という問いが、
- どの空間上で関数が定義されるか?
- その空間の幾何的構造は?
といった幾何・代数・解析の融合領域へと発展していきました。
✅ まとめ:第13問のポイント
- ヒルベルト第13問は、「7次方程式の解を2変数の関数で表現できるか?」という問題。
- 1927年にヴェイユが2変数での代数的関数表現を提示。
- 1957年、アーノルドとコルモゴロフが連続関数の組合せで表現できると証明。
- 「連続関数レベル」では問題は実質解決された。
- ただし「代数的に」完全に2変数で書けるかは依然として議論の余地がある。
- 結果として、この問題は関数論・多様体理論の発展に大きな影響を与えた。
次は第14問へ。実はこれも代数幾何学の深〜い問題なんです!
ヒルベルトの夢の続き、まだまだお付き合いください!
ここまで読んでくださってありがとうございました🙌



