スメイルの18の問題の中でも、特にこの問題12は「一体何を聞いてるの!?」と戸惑う人が多い、超・抽象的な問いです。
最も玄人向けの研いだという言うこともできるでしょう。
でも実はこの問題、「シンプルな動きの中に、どれだけ隠れた対称性があるか?」という、力学系の“隠し味”を探るような話なんです。
ポップに言えば:
「関数Tって、T自身やその反復(T²、T³…)以外に、Tと仲良くできる写像(=可換なもの)っているの?」
「いやいや、TとT²以外は全部“空気読まない”写像だったりしない?」
そんな関数の“孤立性”に関する問題です!
🧩 微分同相写像とは?
まず用語をおさらいしましょう。
✏️ 微分同相写像(diffeomorphism)
簡単に言うと、
「滑らかで、逆写像も滑らかな写像」のこと。
たとえば:
- 実数直線上の関数で、ちゃんと連続していて、微分可能で、
- しかも元に戻せるような(逆写像が存在)関数
これが微分同相写像です。
数学的には、位相空間や多様体の構造を壊さずに変形する“滑らかな変形”と思ってOKです。
以下に出てくる記号のDiffは、この「diffeomorphism(微分同相写像)」の略です。
Diff r (M)と書いたときは、
- r は「r階の微分可能性」を表しています。
- Mは写像が定義されている多様体(空間)です。
♻️ 中心化群(centralizer)とは?
「中心化群」と聞くと難しそうですが、実はこんな内容です。
ある写像 T と“可換”なすべての写像の集合
つまり、
「Tと同時に使っても、順番を入れ替えても結果が変わらない写像たち」
を集めたのが「中心化群(centralizer)」です。
数式で書くと、ある関数 T に対して、
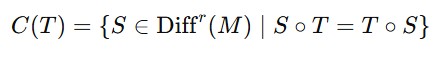
これが Tの中心化群です。
❓問題の核心:孤独な写像っているの?
ここでスメイルが投げかけた疑問は、ずばりこれ:
「TとTⁿ(n回繰り返し)だけしか可換な写像がないTって、たくさんある?」
つまり、「中心化群が“ほぼ自明”なT」が一般的なのか、という話です。
たとえば:
- 「TとT²、T³…」は当然可換
- でもそれ以外に「変なやつ(Tと可換なS)」は近くにいない?
- それとも、Tの周りにはSみたいな“気の合う写像”がたくさんいるの?
スメイルの問いはこれを微分同相写像全体の空間 Diffr(M)\mathrm{Diff}^r(M)Diffr(M) の中で考えたときに、
中心化群が“自明”(=Tの反復しかない)な写像が稠密に存在するか?
というものです。
ちょっとした比喩で理解してみよう!
あなたが主催のダンスイベントで、Tさんというダンサーがいます。
Tさんが踊りだすと、他の人たちが「じゃあ自分も」と動き出す。でも、Tさんは特殊なステップを踏むので、誰とも息が合わない。唯一合わせられるのはTさんのコピーだけ(TさんがT²、T³と繰り返すような人たち)。
そんな「孤高のダンサー」がたくさんいるとわかってきたわけです。
でも、もっと優雅なダンサーの世界(=C²以上)では、まだその孤高さが証明されていません。
果たしてTさんはどの世界でも“唯一無二”でいられるのでしょうか?🕺✨
🧪 解決までの道のり:部分的にクリア!
この難問に対して、2009年に進展がありました!
✅ C¹位相では解決!
- 解決者:Christian Bonatti、Sylvain Crovisier、Amie Wilkinson
- 結果:C¹(1階微分まで連続)という“滑らかさ”の世界では、
中心化群が自明な微分同相写像は稠密に存在することがわかりました!
つまり、
滑らかさが「そこそこ」なら、この孤独な写像はけっこう身近にいる!
ということです。
❓でも、C²以上では?
- 問題は未解決です!
- 微分が2回以上連続(C²やC^∞)のもっと“なめらかすぎる”世界になると、
話が変わってきます。 - そちらでは「孤独な写像」が本当に存在するかどうかはまだ不明。
🧠 解けたら何がわかる?どんな意味があるの?
これ、ぱっと見はニッチすぎる問題に見えますが、実はかなり本質的なテーマです。
🔍 「力学系に隠れた対称性」を知る鍵
- 力学系における構造的安定性や対称性の解析に深く関わる
- カオス vs 安定系の分類や、摂動の影響の解析に応用できる
- 特に、高次元力学系や乱流・天体運動の対称性などへの影響も
🧬 なぜ「中心化群が自明」だと嬉しい?
- その写像が「固有で、他にまねできない動きをしている」ことを意味する
- 「この写像は構造的に独立していて、安定してる」=数理モデルとして理想的
🎯 まとめ(箇条書き)
- 微分同相写像とは、「滑らかで、逆写像も滑らか」な関数
- 中心化群とは、「その写像と可換なすべての写像」の集合
- スメイルの問いは、「中心化群がTⁿ(反復)だけの写像は一般的か?」
- 2009年、C¹位相では“中心化群が自明な写像”が稠密に存在することが判明(Bonattiら)
- しかしC²以上では未解決。より“滑らかな世界”では未知のまま
- この問題は、力学系の安定性や対称性、カオス構造の理解にとって重要な意味を持つ
今回はけっこう抽象的で、小難しい問題でしたね。でも大丈夫。次回はもっと視覚的!『ローレンツアトラクタはストレンジアトラクター?』をカオスと一緒にひも解きます!お楽しみに!



