「正17角形」と聞いて、どう思いますか?
中学や高校の数学で出てくる“作図不可能な多角形”の一つと思われがちですが、実はこれ、定規とコンパスだけで正確に作図できる数少ない高次の正多角形なんです。
とはいえ、教科書的な作図方法は手順が複雑すぎて、とても手軽にできるものではありません。そこで今回は、イギリスの数学者 H. W. リッチモンドの手法をベースに、わずか10分程度で正17角形を描くことができる驚きの作図法をご紹介します。
「正17角形なんて実際に描いたことないよ!」という人も、「ちょっとした幾何学のネタにやってみたい」という人にもおすすめの内容です。
正17角形って、そもそも作図できるの?
「正三角形」や「正六角形」は簡単にコンパスと定規で描けますが、「正17角形」となると、ちょっと話が変わります。
実はこの図形、定規とコンパスだけで作図できる「最大級のレアキャラ」ともいえる存在。
それを最初に証明したのは、かの有名な数学者カール・フリードリッヒ・ガウス。
彼がわずか19歳のときに見つけたこの発見は、あまりにも衝撃的で、「墓石に刻みたい」と言ったほどでした(※実際には刻まれていません)。
正17角形の作図は手数が多すぎる問題
確かに理論的には作図可能なのですが、問題は「手順がめちゃくちゃ多い」こと。
古典的な方法では、
- 角度の精密な分割(21.176…度)
- 無数の補助線と円
- 数十ステップにもおよぶ作図
……と、気軽にやるには骨が折れる作業です。
それでも!「10分でできる作図方法」がある!
そこで登場するのが、H.W.リッチモンド(H.W. Richmond)による簡略化された作図法。
これはなんと、わずか10分ほどの作業で正17角形を描けてしまうという、非常に実用的な方法なんです。
【図なしでもわかる!】正17角形の作図手順(リッチモンド法)
以下はリッチモンドによる作図の概要です。紙とペン、定規とコンパスがあればOK!
🔹 手順①:中心点の設定
直交する2本の線を引き、その交点を円の中心Oとして設定。
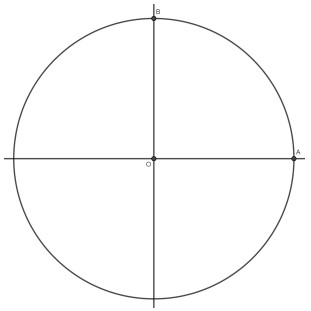
🔹 手順②:線分の二等分を2回繰り返す
線分OBを描き、それを2回二等分し、点Qを得る。
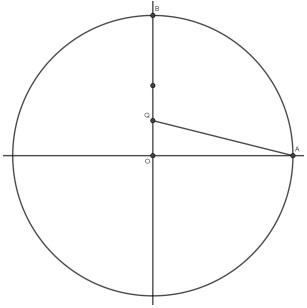
🔹 手順③:角の二等分を2回
点AとQを結び、
- 角OQAをOCで二等分
- 続いて角OQCをODでさらに二等分
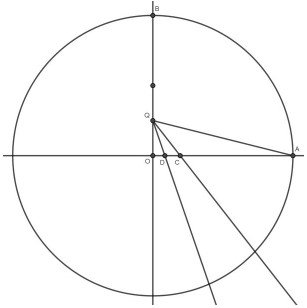
🔹 手順④:垂線と45度の角を作る
- Qから角の二等分線QDに垂直な線QEを引く(QDとQEは直角に交わる直線)
- 角DQEを二等分して、角DQF(=45度)を作る
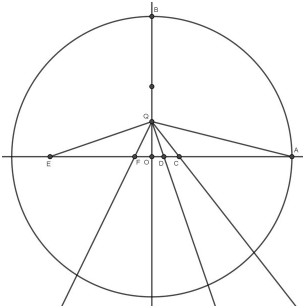
🔹 手順⑤:円と接線で頂点を見つける
- 線AFを直径とした半円を描き、OBとの交点Gを得る
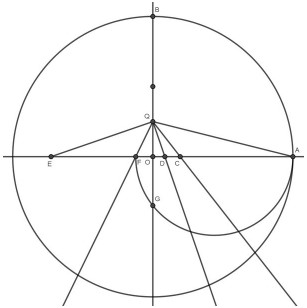
- 点Dを中心に、DGの半径で円を描く
- 線EAに垂直な接線を2本引く
→ それぞれが正17角形の頂点を含む点に到達(Aも頂点の一つになります)
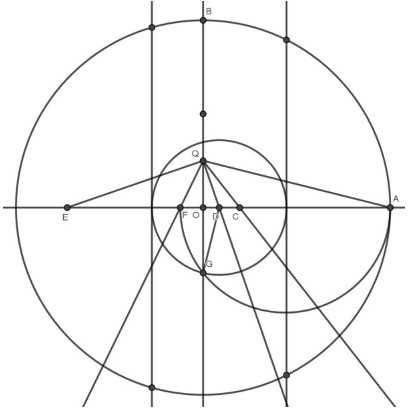
🔹 手順⑥:残りの頂点を回転で求める
最初に得た数点を基準に、コンパスで等間隔に円周をコピーして、全17頂点を取得!

これで正17角形が完成します!
なんでこの方法で正17角形ができるの?
ポイントは、
- 二段階の角の二等分で21.176度相当の角度を作り出すこと
- 補助線と円の配置で幾何学的に条件を満たす点を構築すること
という、幾何学的な知恵の結晶にあります。
リッチモンドの方法のポイント
リッチモンドの手法では、以下のようなシンプルな幾何操作で、21.1765°を含む角度を作り出していきます。
- 角の二等分(二回)と線分の二等分(二回)
→ この操作で特定の比率や点を得ます。 - 45度の角を作って、それをさらに二等分
→ これにより、21度台に近い角度を作成。 - 円と接線を使って、正17角形の頂点を順に決定
→ 幾何学的な対称性を利用して、17等分した点を次々に見つけられる。
まとめ:正17角形は意外と簡単に描ける
最後に、今回の内容をポイントで振り返りましょう:
✅ 本文の要約
- 正17角形は定規とコンパスだけで作図できる珍しい図形で、最初に証明したのはガウス
- しかし通常の作図は非常に手順が多く、実際に描くのは大変
- H.W.リッチモンドの方法を使えば、10分ほどで現実的に作図が可能
- 手順の特徴は、線分や角の二等分、45度の角、円と接線の活用など
- 幾何的な構造を使って21.176度(360 ÷ 17)に相当する角度を構築するのがカギ
🧭 あなたもチャレンジしてみよう!
紙とコンパスがあれば、誰でも天才ガウスの発見を“体感”できます。
数学が苦手でも大丈夫!手順通りに線を引いていくだけで、17の頂点があなたの手に。