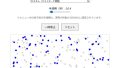
角運動量保存則のシミュレーションをウェブ上で実行し、各速度の変化などが観察できるサイトツールです。
上の埋め込み内でも使えますが、うまく動かない・大きなページで使いたいというときは、元の角運動量保存則シミュレーションページへ(新しいタブで開きます)。
角運動量保存則とは?
角運動量とは、「回転している物体が持つ勢い」のことです。
直線運動における運動量(質量×速度)と同じように、
回転運動にも「質量」や「速さ(角速度)」、「回転の半径」が関係しています。
角運動量 L の式は次のとおり:
L = m × r² × ω
- L:角運動量
- m:質量
- r:回転半径
- ω(オメガ):角速度(ラジアン毎秒)
この「角運動量 L」は、外部からトルク(回転させる力)が加わらなければ変化しません。
つまり、
ある物体が回転していても、回転半径や質量が変わっても、角運動量は一定に保たれるのです。
🌀 例:スケート選手の回転
スケート選手が腕を広げた状態から、ぐっと引き寄せると回転が速くなる――
これはまさに、角運動量が保存されている例です。
- 半径(腕の長さ)が小さくなることで
- 回転の速さ(角速度)が大きくなる
結果として、L の値は変わらずに保たれます。
この法則を、実際に体験してみましょう!
🖥 ツールの使い方
以下のシミュレーションでは、質量のある粒子が円運動している様子が表示されます。
初期条件を調整して、「角運動量保存」がどう働くのか、視覚的に理解することができます。
🛠 操作方法
- 質量 m (kg)
スライダーで回転する物体の質量を設定します(0.1~5kg) - 初期半径 r (px)
中心から物体までの初期の距離を設定します(50~150ピクセル) - 初期角速度 ω (rad/s)
回転を開始する際の角速度を設定します(0.1~10 rad/s) - スタートボタンを押す
円運動が始まります。
青い粒子が回転し、中心との間に線が引かれます。
回転中に半径を変えると、角速度が自動で変化します。
これは、角運動量 L を一定に保つためです。
- ストップボタンを押すと停止
再度「スタート」を押すと、同じLのまま再開されます。
📊 表示される情報
シミュレーションの下には、リアルタイムで以下の値が表示されます:
- 角速度 ω(オメガ)
- 半径 r
- 角運動量 L = m × r² × ω
スライダーを操作するたびに、自動で再計算され、画面にも反映されます。
物理的な計算式と動きがリンクしているので、直感的に理解が進みます。
📌 まとめ
このツールは、角運動量保存の原理を体験的に学べるシミュレーションです。
改めて、ポイントを整理します:
- 角運動量 L = m × r² × ω という式に基づいて、回転運動を表現
- 外力(トルク)がない場合、角運動量は常に保存される
- スケート選手の動きなど、日常の現象にもこの法則が関係
- このツールでは、半径を変えると角速度が変化することでLを保存
- 質量・半径・角速度は、スライダーで直感的に操作可能
- 数式とグラフィックを同時に見ることで、学習効果が高まる
このような「見る物理」「動かす物理」は、教科書だけでは得られない理解を助けてくれます。
ぜひ何度も試してみて、いろいろなパターンで角運動量の変化と保存を体感してみてください。