こんにちは!「ヒルベルトの23の問題を全部解説するまで帰れない」シリーズ、いよいよ第21問。
今回はちょっとクセが強い問題、「モノドロミー群」と「線型微分方程式」のお話です。
名前の圧だけでもう「なんか難しそう…」ってなるかもしれませんが、
実はこの問題、“一度は解けたと思われたけど、実は解けてなかった”という珍しい歴史をもっています。
今回はその顛末も含めて、たっぷりご紹介します!
🤔モノドロミー群って何?
数学の世界では、関数の“クセ”を捉える道具として「群(group)」がよく使われます。
モノドロミー群とは、「複素平面をぐるっと回ったときに、解がどう変化するか」という現象を捉える群です。
たとえば、複素対数関数 log(z) は、1周すると 2πi ずれます。これが「モノドロミー」的な振る舞いの典型例です。
この変化が行列の変換として表され、それらが満たす性質全体が「モノドロミー群」と呼ばれます。
📘線型微分方程式とは?
「未知の関数」とその「導関数」の間に線形の関係があるような微分方程式を言います。
たとえば、
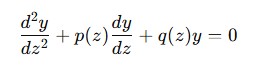
のような式ですね。係数 p(z),q(z)が複素関数であれば、これは複素領域における線型微分方程式になります。
ヒルベルト第21問では、特にフックス型と呼ばれる「特異点の性質がよく管理された微分方程式」に注目しています。
🔍ヒルベルト第21問題とは?
この問題のテーマは、19世紀から続く有名な問い、
リーマン・ヒルベルト問題(Riemann–Hilbert problem)
にあたります。
問いの内容はざっくり言うとこう:
「複素平面上に有限個の特異点をもつ正則な線型微分方程式で、与えられたモノドロミー群を実現するような方程式を常に構成できるか?」
つまり、モノドロミー群の“逆算”が可能か、ということです。
🛤️解決までの道のり:一度は「勝利」かと思いきや…
🟢1908年:プレメルヒの勝利!
クロアチアの数学者ジョシップ・プレメルヒは、問題を積分方程式のかたちに書き換えることで、この問題を肯定的に証明しました。
「任意のモノドロミー表現に対応するフックス型の線型微分方程式は存在する」と主張したこの証明は、
その後長らく「解決済み」として受け入れられました。
🟢1913年:バーコフも別証明!
アメリカのG. D. Birkhoff(バーコフ)も、別ルートから同様の結論に到達。
これにより「第21問は完全に解決された」と考えられていたのです。
💥…しかし!1980年代に暗雲が立ち込める
プレメルヒの証明は一見エレガントでしたが、実は厳密性に欠ける点がありました。
🚨1989年:アノゾフとボリブルヒが反証!
ソビエトの数学者ドミトリー・アノゾフとアンドレイ・ボリブルヒは、
- 一般には、与えられたモノドロミー群に対応する正則なフックス型微分方程式が存在しない場合がある
ということを示しました。
特に、
- モノドロミー表現が既約(分解できない)である場合に限っては肯定的に成り立つが、
- 一般の(可約な)場合には成り立たない!
という条件付きの答えが提示されたのです。
これは、プレメルヒとバーコフの証明が実は限定的なケースしか扱っていなかったことを意味していました。
🔍補足:なぜこれが重要なの?
モノドロミー群の逆問題は、現代でも、
- 複素微分幾何
- 表現論
- 数理物理(特に量子場理論)
など、さまざまな分野で極めて重要です。
また、これに近いアイデアは、「パラメトリックなモノドロミー問題」や「等質空間上の構造理論」などにも波及しており、
数学の本質的な「構造の対応関係」に深く関わっています。
🧠第21の問題が残したもの
この問題が数学界に残した最大の教訓は、次の2点です:
- 「一見うまくいっているように見える証明」でも、細部に罠が潜むことがある
- 条件付きの存在定理が、どこまで許容されるかは時代によって変わる
さらに、この問題は、
- 問いの“再定式化”がいかに大事か
- 一般の命題に対して「どの条件で成立するか」を問い直す必要があること
を強く示しています。
✅まとめ
- 第21問題は「モノドロミー群をもつ微分方程式がいつも存在するか?」という問題。
- 一度はプレメルヒとバーコフによって「解決された」とされた。
- しかし1989年にアノゾフとボリブルヒが反例を発見し、問題は“否定的に解決”された。
- 特定条件下(既約な場合)でのみ肯定的な解答が成立する。
- 数学において「問いの定義」「証明の厳密性」「条件付き成立の意味」などを考え直す好例でもある。
このように、第21問は「解けたと思ったら解けてなかった…でも深くて面白い」問題です。
次回は、第22問に突入!残りあとわずか…終盤戦、どんどん盛り上がっていきます!



