 サイトツール
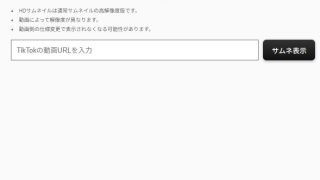
サイトツール TikTok動画サムネイル取得/表示/保存サイトツール-URLからサムネ表示
TikTokの動画のサムネイルを、動画URLから取得、表示してくれるサイトツールです。保存も可能です。上の埋め込み内でも使えますが、うまく動かない・大きなページで使いたいというときは、元のTikTok動画サムネイル取得・表示ツールページへ(...
 サイトツール
サイトツール  ゲーム
ゲーム  サイトツール
サイトツール  サイトツール
サイトツール  サイトツール
サイトツール  サイトツール
サイトツール  サイトツール
サイトツール  サイトツール
サイトツール  都市伝説調査隊
都市伝説調査隊  サイトツール
サイトツール  サイトツール
サイトツール  映画元ネタ
映画元ネタ  サイトツール
サイトツール  サイトツール
サイトツール  サイトツール
サイトツール 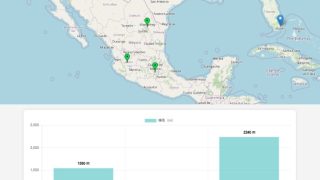 サイトツール
サイトツール 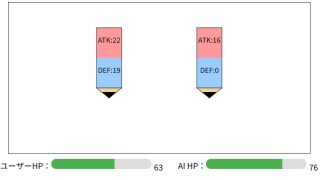 サイトツール
サイトツール  サイトツール
サイトツール  サイトツール
サイトツール  サイトツール
サイトツール