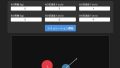
数学の未解決問題であるコラッツ予想(コラッツの問題)のシミュレーションをウェブ上で実行して、値の変化を観察できるサイトツールです。
上の埋め込み内でも使えますが、うまく動かない・大きなページで使いたいというときは、元のコラッツ予想シミュレーションページへ(新しいタブで開きます)。
コラッツ予想(コラッツの問題)とは?
コラッツ予想は、1930年代に提唱された数学の未解決問題の一つです。
簡単にいうと、
「どんな正の整数から始めても、次のルールに従って数を計算すると、最終的に1に到達する」
という予想です。
具体的なルールは以下の通りです。
- 数字が偶数なら、2で割る。
- 数字が奇数なら、3倍して1を足す。
これを繰り返すと、どんな数でもやがて1になると予想されています。
しかし、この予想はまだ完全に証明されていません。
コラッツ予想シミュレーション 使い方
1. 初期値の入力
画面中央の「初期値(2〜1000)」の入力欄に、任意の整数を入力します。
ここで入力できるのは「2」から「1000」までの整数です。
入力が範囲外だったり、数値以外が入っているとアラートで注意されるので、必ず範囲内の数字を入れてください。
2. スタートボタンでシミュレーション開始
初期値を入力したら、その隣にある「スタート」ボタンを押します。
これでコラッツ数列の計算が始まり、キャンバスにグラフが表示されます。
グラフの横軸はステップ数(数列の何番目か)、縦軸はそのステップの数値を表しています。
数列の値が変化していく様子が線で繋がれて、アニメーションで順に表示されます。
3. リセットボタンでキャンバスをクリア
計算結果をクリアしたい場合は、「リセット」ボタンを押します。
キャンバスの描画が消えて、入力欄も初期値の「27」に戻ります。
新しい値で再度シミュレーションをしたいときに使いましょう。
4. 結果の見方
アニメーションが終わると、キャンバスの下の「結果表示エリア」に
「ステップ数 XX で1に到達しました。」
と表示されます。
これがその初期値から1にたどり着くまでに必要なステップ数です。
グラフの見方のポイント
- グラフの左端の赤い点はスタートの数値を示します。
- 黒い線と点は数列の途中の値をつないでいます。
- 最後の青い点が「1」に到達した地点です。
- 横軸は計算ステップ数で、縦軸はそのステップの値。
- 縦軸の目盛りは最大値に応じて10や100刻みで表示され、見やすく調整されています。
コラッツ予想シミュレーションツール まとめ
- コラッツ予想は「どんな数でも決められたルールで計算すると最終的に1に到達する」という未解決問題。
- 初期値を「2〜1000」の範囲で入力する。
- 「スタート」ボタンでコラッツ数列の生成とアニメーション開始。
- グラフ上で数列の変化を視覚的に追える。
- 「リセット」ボタンでクリアして、再入力できる。
- アニメーション終了後にステップ数の結果が表示される。
このシミュレーションは、数学的に難しいコラッツ予想を理解するための助けになります。
数列の動きを実際に見てみることで、変化のパターンや収束の仕方を体感的に学べるでしょう。
ぜひ色々な初期値を試して、面白い数列の挙動を楽しんでみてください!