五目並べはだれしも遊んだことのあるボードゲームですが、これについてはジャーナリストの黒岩涙香が必勝法を発見したということが知られています。ここでは、黒岩涙香が発見した五目並べの必勝法について解説していきます。
黒岩涙香の五目並べの必勝法とは?
五目並べは手軽にできるボードゲームとしてとても有名です。
これについて多少調べたことのある人なら、「黒岩涙香というジャーナリストが必勝法を発見し、その後にルールを再整備して五目並べの亜種である『連珠』が作られた」という事実を聞きかじった人も多いと思います。

ですが、調べてもその必勝法がどんなものかはわからないことが多く、謎でした。
黒岩涙香(くろいわ るいこう)の五目並べの必勝法は、以下の文献「聯珠真理 : 一名・五目並べ先手全勝法」で述べられています。

ここでは、英語の文献などを調べてわかった黒岩涙香の必勝法についてできる限り解説していきます。
黒岩涙香の必勝法は、「手の強制」が重要ポイント
黒岩涙香の必勝法を知るには、「手の強制」という要素が重要です。
例えば、黒が3つ並べた場合、この直後に白が両端どちらかの隣に置かないと、負けが確定します。
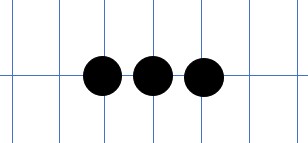
また、黒が4つ並べた場合、片側がふさがっていたとしても、この直後にもう片方に置かないと、負けが確定します。(片側すらふさがっていないと、白の負けが確定。)
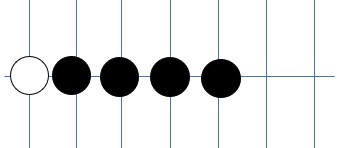
これを黒の視点でいうと、「相手の手を強制的に特定の場所に誘導することができる」ということになります。
黒岩涙香が発見したのは、
「ゲームの途中から黒が”手の強制”を連続させることができ、白は強制された場所に置いているうちにリーチが複数できて結局負けてしまう」
ということのようです。
ちなみに、黒岩涙香は考えうるゲーム展開を数え上げる形で追っていき、黒が必勝であることを示したようです。
黒岩涙香の五目並べの必勝法!
ここからは、黒岩涙香の五目並べの必勝法をゲームの途中から見ていきます。
以下では、黒白それぞれの手が番号で表示されています。黒が21番に打ったところで3つの並びが形成され、「手の強制」がここから連続で始まります。
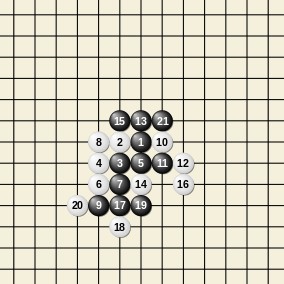
この直後、白は22番の手で15か21の横に置かないと、負けが確定します。ここでは15の横に置いたとしてそのあとの動向を見ていきます。
すると、図のように、黒は23に置くことで斜めに4つの並びが作れます。そして白は強制的に24でそれを防ぐしかありません(片側はすでにふさがっているが、もう一方に置かないと負ける)。
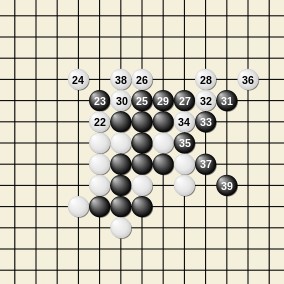
以下同様に、黒は25で4つの並び、27で4つの並び、29で両端がふさがっていない3つの並び、31で4つの並び、33で4つの並び、35で4つの並びを作ることができ、白の手を強制させることができます。
そして、37でどちらもふさがっていない4つの並びを作ることで白の負けが確定します。
そして、白は38に置くものの、反対側がふさがっていないので黒が39で斜めに5つの並びを作って、黒の勝ちになります。
これは最初に21の横においても、連続で手の強制を起こすことができ、白の負けになります。
つまり、どのようにやっても、黒による手の強制が途中から連続で起きてしまうので、黒が必勝ということになります。
これを経験的に知っている上級者は、どのように遊んでもおおよそ40ムーブ(黒20手、白20手)以内に勝つことができるようです。
禁じ手の整備で連珠の誕生へ
上で見たように、禁じ手なしの五目並べでは、明らかに黒に勝利が偏ります。
黒岩涙香は、これをなるべく均等にするために、禁じ手を作ってルールを整備しなおし、五目並べの派生形である『連珠』を作りました。
連珠の禁じ手
連珠の禁じ手はいくつかありますが、有名なのは以下のようなものです。
三三・・・同じ点の周りに3つの並びが同時に2つ以上できること。
四四・・・同じ点の周りに4つの並びが同時に2つ以上できること。
これらは黒が作った場合は反則負けになりますが、白は作っても反則にはなりません。
こうしてみてみると、五目並べの欠点をうまく回避していることがわかります。
まとめ
- 黒岩涙香が発見した五目並べの必勝法は、手番を数え上げることで黒が連続で手の強制ができるということを示したもの。
- 黒が途中から連続で白の手を強制させることができるのは、3つの並び、4つの並びを理解すればある程度直観的に理解できる。
- 黒の優位性を下げて公平にしたのが連珠であり、三三などの黒が対象の禁じ手がある。
黒岩涙香の五目並べの必勝法については、昔から疑問に思っていましたが、今回調べてみて、一応理解できてよかったです。



